题目内容
18.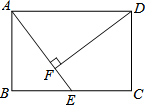 如图,在矩形ABCD中,E是BC边的中点,DF⊥AE,垂足为F.
如图,在矩形ABCD中,E是BC边的中点,DF⊥AE,垂足为F.(1)求证:△ADF∽△EAB.
(2)若AB=4,AD=6,求DF的长.
分析 (1)由矩形的性质得出AD=BC,AD∥BC,∠B=90°,由平行线的性质得出∠DAF=∠AEB,证出∠AFD=∠B,即可得出结论;
(2)由勾股定理求出AE,由相似三角形的性质得出对应边成比例,即可求出DF的长.
解答 (1)证明:∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,∠B=90°,
∴∠DAF=∠AEB,
∵DF⊥AE,
∴∠AFD=90°=∠B,
∴△ADF∽△EAB.
(2)解:∵BC=AD=6,E是BC边的中点,
∴BE=3,
∴AE=$\sqrt{{3}^{2}+{4}^{2}}$=5,
由(1)得:△ADF∽△EAB,
∴$\frac{DF}{AB}=\frac{AD}{AE}$,
即$\frac{DF}{4}=\frac{6}{5}$,
解得:DF=$\frac{24}{5}$.
点评 本题考查了相似三角形的判定与性质、矩形的性质、勾股定理、平行线的性质;熟练掌握矩形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
相关题目
8.若抛物线y=x2+(m-1)x+(m+3)的顶点在坐标轴上,则m的值有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
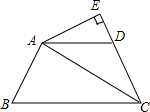 已知四边形ABCD中,AB=AD,CA平分△BCD,AE⊥CD交CD延长线于E.请问线段BC,CE及DE间有何关系?说明理由.
已知四边形ABCD中,AB=AD,CA平分△BCD,AE⊥CD交CD延长线于E.请问线段BC,CE及DE间有何关系?说明理由.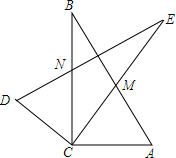 两个形状大小完全一样的两个Rt△ACB和Rt△DCE如图放置,设两直角边BC、CE的夹角∠ECB=α,∠A=β.
两个形状大小完全一样的两个Rt△ACB和Rt△DCE如图放置,设两直角边BC、CE的夹角∠ECB=α,∠A=β.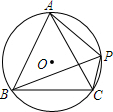 如图,在⊙0中,$\widehat{AB}$=$\widehat{AC}$,点P为弧AC上一点,且∠BPC=60°.若BP=6,PC=2.求线段AP的长度.
如图,在⊙0中,$\widehat{AB}$=$\widehat{AC}$,点P为弧AC上一点,且∠BPC=60°.若BP=6,PC=2.求线段AP的长度.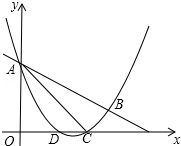 如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).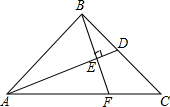 如图,在Rt△ABC中,∠ABC=90°,点D为BC边上的点,BE⊥AD于点E,延长
如图,在Rt△ABC中,∠ABC=90°,点D为BC边上的点,BE⊥AD于点E,延长 如图,锐角△ABC的外接圆O.在BC边上取两点D、E使∠BAD=∠CAE,EM⊥AB于点M,EN⊥AC于点N,AD的延长线交⊙O于点P.求证:AP•MN=AB•AC•sin∠BAC.
如图,锐角△ABC的外接圆O.在BC边上取两点D、E使∠BAD=∠CAE,EM⊥AB于点M,EN⊥AC于点N,AD的延长线交⊙O于点P.求证:AP•MN=AB•AC•sin∠BAC.