题目内容
4.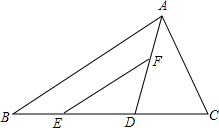 已知,如图△ABC中,AD平分∠BAC,DE=DC,EF∥AB.求证:AC=EF.
已知,如图△ABC中,AD平分∠BAC,DE=DC,EF∥AB.求证:AC=EF.
分析 由三角形的角平分线定理得:$\frac{AC}{AB}=\frac{CD}{BD}$,由EF∥AB,推出△DEF∽△DAB,根据相似三角形的性质得到$\frac{EF}{AB}=\frac{DE}{BD}$,等量代换得到$\frac{AC}{AB}=\frac{EF}{AB}$,于是得到结论.
解答 证明:∵AD平分∠BAC,
由三角形的角平分线定理得:$\frac{AC}{AB}=\frac{CD}{BD}$,
∵EF∥AB,
∴△DEF∽△DAB,
∴$\frac{EF}{AB}=\frac{DE}{BD}$,
∵DE=DC,
∴$\frac{AC}{AB}=\frac{EF}{AB}$,
∴AC=EF.
点评 本题考查了相似三角形的判定和性质,三角形角平分线定理,熟练掌握三角形的角平分线定理是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 已知如图,点D在CB延长线上,E在AB上,连接DE,若∠DEB=∠A,点B为DC中点.求证:DE=AC.
已知如图,点D在CB延长线上,E在AB上,连接DE,若∠DEB=∠A,点B为DC中点.求证:DE=AC.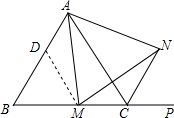 如图,在等边三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点.若∠AMN=60°,求证:AM=MN.
如图,在等边三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点.若∠AMN=60°,求证:AM=MN.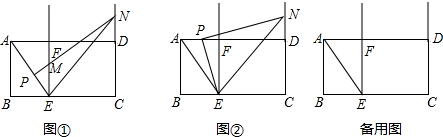
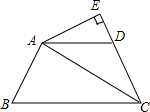 已知四边形ABCD中,AB=AD,CA平分△BCD,AE⊥CD交CD延长线于E.请问线段BC,CE及DE间有何关系?说明理由.
已知四边形ABCD中,AB=AD,CA平分△BCD,AE⊥CD交CD延长线于E.请问线段BC,CE及DE间有何关系?说明理由. 两个形状大小完全一样的两个Rt△ACB和Rt△DCE如图放置,设两直角边BC、CE的夹角∠ECB=α,∠A=β.
两个形状大小完全一样的两个Rt△ACB和Rt△DCE如图放置,设两直角边BC、CE的夹角∠ECB=α,∠A=β. 如图,锐角△ABC的外接圆O.在BC边上取两点D、E使∠BAD=∠CAE,EM⊥AB于点M,EN⊥AC于点N,AD的延长线交⊙O于点P.求证:AP•MN=AB•AC•sin∠BAC.
如图,锐角△ABC的外接圆O.在BC边上取两点D、E使∠BAD=∠CAE,EM⊥AB于点M,EN⊥AC于点N,AD的延长线交⊙O于点P.求证:AP•MN=AB•AC•sin∠BAC.