题目内容
12. 如图,直线x=2与y=x+a的交点A在第四象限,则a的取值范围是a<-2.
如图,直线x=2与y=x+a的交点A在第四象限,则a的取值范围是a<-2.
分析 首先把x=2和y=x+a组成方程组,求解,根据题意交点坐标在第四象限表明y小于0,即可求得a的取值范围.
解答 解:解方程组$\left\{\begin{array}{l}{x=2}\\{y=x+a}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=2+a}\end{array}\right.$,
∵直线y=2x与y=-x+k的交点在第四象限,
∴2+a<0,
故答案为:a<-2.
点评 本题主要考查两直线相交的问题,关键在于解方程组求出x、y,根据在第四象限的点坐标性质解不等式.

练习册系列答案
相关题目
20. 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A. | 美 | B. | 丽 | C. | 广 | D. | 州 |
17.-2017绝对值是( )
| A. | -2017 | B. | 2017 | C. | $\frac{1}{2017}$ | D. | 0 |
4.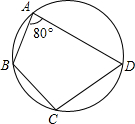 如图,四边形ABCD内接于⊙O,∠BAD=80°,若弧ABC与弧ADC的长度分别为7π,11π,则弧BAD的长度为( )
如图,四边形ABCD内接于⊙O,∠BAD=80°,若弧ABC与弧ADC的长度分别为7π,11π,则弧BAD的长度为( )
 如图,四边形ABCD内接于⊙O,∠BAD=80°,若弧ABC与弧ADC的长度分别为7π,11π,则弧BAD的长度为( )
如图,四边形ABCD内接于⊙O,∠BAD=80°,若弧ABC与弧ADC的长度分别为7π,11π,则弧BAD的长度为( )| A. | 9π | B. | 10π | C. | 11π | D. | 12π |
2. 如图所示,小华从A点出发,沿直线前进10米后左转20°,再沿直线前进10米,又向左转20°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
如图所示,小华从A点出发,沿直线前进10米后左转20°,再沿直线前进10米,又向左转20°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
 如图所示,小华从A点出发,沿直线前进10米后左转20°,再沿直线前进10米,又向左转20°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
如图所示,小华从A点出发,沿直线前进10米后左转20°,再沿直线前进10米,又向左转20°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )| A. | 200米 | B. | 180米 | C. | 160米 | D. | 140米 |