题目内容
4．
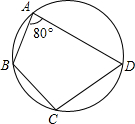如图，四边形ABCD内接于⊙O，∠BAD=80°，若弧ABC与弧ADC的长度分别为7π，11π，则弧BAD的长度为（ ）| A． | 9π | B． | 10π | C． | 11π | D． | 12π |
分析 设⊙O的半径为r，根据弧ABC与弧ADC的长度分别为7π，11π求出r的值，再根据圆内接四边形的性质求出∠C的度数，利用弧长公式即可得出结论．
解答 解：设⊙O的半径为r，
∵弧ABC与弧ADC的长度分别为7π，11π，
∴7π+11π=2πr，解得r=9．
∵∠BAD=80°，
∴∠C=180°-80°=100°，
∴$\widehat{BAD}$所对的圆心角是200°，
∴弧BAD的长度=$\frac{200π×9}{180}$=10π．
故选B．
点评 本题考查的圆内接四边形的性质，熟知圆内接四边形的对角互补是解答此题的关键．
练习册系列答案
相关题目
15．
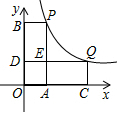如图，在平面直角坐标系中，点P（1，5），Q（m，n）在反比例函数的图象上，过点P分别作x轴、y轴的垂线，垂足为点A，B；点Q为图象上的动点，过点Q分别作x轴、y轴的垂线，垂足分别为点C、D，两垂线相交于点E，随着m的增大，四边形OCQD与四边形OAPB不重合的面积变化为（ ）
如图，在平面直角坐标系中，点P（1，5），Q（m，n）在反比例函数的图象上，过点P分别作x轴、y轴的垂线，垂足为点A，B；点Q为图象上的动点，过点Q分别作x轴、y轴的垂线，垂足分别为点C、D，两垂线相交于点E，随着m的增大，四边形OCQD与四边形OAPB不重合的面积变化为（ ）| A． | 先增大后减小 | B． | 先减小后增大 | ||
| C． | 先减小后增大再减小 | D． | 先增大后减小再增大 |
如图，直线x=2与y=x+a的交点A在第四象限，则a的取值范围是a＜-2．
19．下列运算正确的是（ ）
| A． | （x3）2=x5 | B． | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | C． | （x+1）2=x2+1 | D． | x3•x2=x5 |
13．点A在x轴的下方，y轴的右侧，到x轴的距离是3，到y轴的距离是2，则点A的坐标是（ ）
| A． | （2，-3） | B． | （2，3） | C． | （3，-2） | D． | （-3，-2） |