题目内容
对于反比例函数y=
(k≠0),下列说法错误的是( )
| k2 |
| x |
| A、它的图象分布在第一、三象限 |
| B、y随x的增大而减小 |
| C、它的图象是中心对称图形 |
| D、点(k,k)在它的图象上 |
考点:反比例函数的性质
专题:
分析:先判断出k2的符号,再根据反比例函数的性质即可得出结论.
解答:解:A、∵k≠0,∴k2>0,∴它的图象分布在第一、三象限,故本选项正确;
B、∵它的图象分布在第一、三象限,∴在每一象限内y随x的增大而减小,故本选项错误;
C、∵此函数是反比例函数,∴它的图象是中心对称图形,故本选项正确;
D、∵k•k=k2,∴点(k,k)在它的图象上,故本选项正确.
故选B.
B、∵它的图象分布在第一、三象限,∴在每一象限内y随x的增大而减小,故本选项错误;
C、∵此函数是反比例函数,∴它的图象是中心对称图形,故本选项正确;
D、∵k•k=k2,∴点(k,k)在它的图象上,故本选项正确.
故选B.
点评:本题考查的是反比例函数的性质,熟知反比例函数y=
(k≠0)中,当k>0时函数图象的两个分支分别位于一三象限是解答此题的关键.
| k |
| x |

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
下列运算正确的是( )
| A、-a-1=-(a-1) |
| B、(-a3)2=a6 |
| C、(a-b)2=a2-b2 |
| D、3a3-2a2=a3 |
下列计算正确的是( )
| A、(a-b)2=a2-b2 |
| B、a2+a2=2a2 |
| C、(a3)2=a5 |
| D、a2•a2=2a2 |
x<0,y>0时,则x,y,0中最大的数是( )
| A、x | B、y | C、0 | D、没有 |
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,⊙O的半径是5,sinB=
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,⊙O的半径是5,sinB=| 2 |
| 5 |
| A、2 | B、3 | C、4 | D、5 |
 如图,AB=BC=CD,∠A=25°,则∠BCD=
如图,AB=BC=CD,∠A=25°,则∠BCD=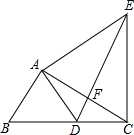 如图,把△ABC绕点A旋转得到△ADE(D与E重合),当点D刚好落在BC上时,连接CE,设AC、DE相交于点F,则图中相似三角形的对数是( )
如图,把△ABC绕点A旋转得到△ADE(D与E重合),当点D刚好落在BC上时,连接CE,设AC、DE相交于点F,则图中相似三角形的对数是( )