题目内容
 如图,Rt△ABC中,∠C=90°,D是BC上一点,AD=BD,tan∠ADC=
如图,Rt△ABC中,∠C=90°,D是BC上一点,AD=BD,tan∠ADC=| 4 |
| 3 |
| 5 |
考点:解直角三角形
专题:计算题
分析:在Rt△ACD中,根据正切的定义得到tan∠ADC=
=
,设AC=4x,CD=3x,根据勾股定理得AD=5x,则BD=AD=5x,所以BC=BD+CD=8x,在Rt△ABC中,根据勾股定理得到AB=4
x,于是有4
x=4
,解得x=1,所以CD=3.
| AC |
| CD |
| 4 |
| 3 |
| 5 |
| 5 |
| 5 |
解答:解:在Rt△ACD中,tan∠ADC=
=
,
设AC=4x,CD=3x,
∴AD=
=5x,
∴BD=AD=5x,
∴BC=BD+CD=8x,
在Rt△ABC中,AC=4x,BC=8x,
∴AB=
=4
x,
而AB=4
,
∴4
x=4
,
解得x=1,
∴CD=3x=3.
故答案为3.
| AC |
| CD |
| 4 |
| 3 |
设AC=4x,CD=3x,
∴AD=
| AC2+CD2 |
∴BD=AD=5x,
∴BC=BD+CD=8x,
在Rt△ABC中,AC=4x,BC=8x,
∴AB=
| AC2+BC2 |
| 5 |
而AB=4
| 5 |
∴4
| 5 |
| 5 |
解得x=1,
∴CD=3x=3.
故答案为3.
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
相关题目

 如图,点A为x轴负半轴上一点,点B为x轴正半轴上一点,OA,OB(OA<OB)的长分别是关于x的一元二次方程x2-4mx+m2+2=0的两根,C(0,3),且S△ABC=6,则∠ABC的度数为
如图,点A为x轴负半轴上一点,点B为x轴正半轴上一点,OA,OB(OA<OB)的长分别是关于x的一元二次方程x2-4mx+m2+2=0的两根,C(0,3),且S△ABC=6,则∠ABC的度数为 如图,AB=BC=CD,∠A=25°,则∠BCD=
如图,AB=BC=CD,∠A=25°,则∠BCD=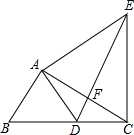 如图,把△ABC绕点A旋转得到△ADE(D与E重合),当点D刚好落在BC上时,连接CE,设AC、DE相交于点F,则图中相似三角形的对数是( )
如图,把△ABC绕点A旋转得到△ADE(D与E重合),当点D刚好落在BC上时,连接CE,设AC、DE相交于点F,则图中相似三角形的对数是( )