题目内容
12.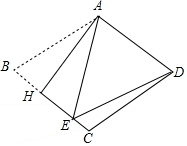 如图,把菱形ABCD沿AH折叠,B落在BC边上的点E处.若∠BAE=40°,则∠EDC的大小为( )
如图,把菱形ABCD沿AH折叠,B落在BC边上的点E处.若∠BAE=40°,则∠EDC的大小为( )| A. | 10° | B. | 15° | C. | 18° | D. | 20° |
分析 根据翻折变换的性质可得AB=AE,然后根据等腰三角形两底角相等求出∠B=∠AEB=70°,根据菱形的四条边都相等可得AB=AD,菱形的对角相等求出∠ADC,再求出∠DAE,然后根据等腰三角形两底角相等求出∠ADE,然后根据∠EDC=∠ADC-∠ADE计算即可得解.
解答 解:∵菱形ABCD沿AH折叠,B落在BC边上的点E处,
∴AB=AE,
∵∠BAE=40°,
∴∠B=∠AEB=$\frac{1}{2}$(180°-40°)=70°,
在菱形ABCD中,AB=AD,∠ADC=∠B=70°,
AD∥BC,
∴∠DAE=∠AEB=70°,
∵AB=AE,AB=AD,
∴AE=AD,
∴∠ADE=$\frac{1}{2}$(180°-∠DAE)=$\frac{1}{2}$(180°-70°)=55°,
∴∠EDC=∠ADC-∠ADE=70°-55°=15°.
故选B.
点评 本题考查了翻折变换的性质,菱形的性质,等腰三角形两底角相等的性质,翻折前后对应边相等,菱形的四条边都相等,对角相等.

练习册系列答案
相关题目
2.下列计算正确的是( )
| A. | a-1•a-3=a3 | B. | (a-2)2=a4 | C. | a2÷a-4=a-2 | D. | (-2a)3=-8a3 |
3.下列各数属于用科学记数法表示的是( )
| A. | 41.5×105 | B. | 0.413×104 | C. | -12×104 | D. | -7.16×105 |
20.一个角的两边分别平行于另一个角的两边,则这两个角( )
| A. | 相等 | B. | 相等或互补 | C. | 互补 | D. | 不能确定 |
7.直线y=-x-2与两坐标轴围成的图形的面积是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
17.下列所给数中,是无理数的是( )
| A. | 2 | B. | $\frac{2}{7}$ | C. | 0.$\stackrel{•}{2}$ | D. | $\sqrt{2}$ |
4.实数$\frac{{\sqrt{2}}}{2}$,-$\frac{3}{7}$,0.1010010001,$\root{3}{4}$,π,$\sqrt{144}$中,无理数的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
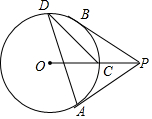 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧AB上不与点A、点B重合的一个动点,连接AD、CD,若∠APB=76°,则△ADC的度数为( )
如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧AB上不与点A、点B重合的一个动点,连接AD、CD,若∠APB=76°,则△ADC的度数为( )