题目内容
9.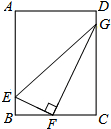 如图,矩形ABCD中,E、G为AB、CD边上的点,F为BC的中点,且BE=1,CG=4,EF⊥FG.
如图,矩形ABCD中,E、G为AB、CD边上的点,F为BC的中点,且BE=1,CG=4,EF⊥FG.(1)求证:△EBF∽△FCG;
(2)求EG的长.
分析 (1)由四边形ABCD是矩形,于是得到∠B=∠C=90°,根据余角的性质得到∠EFB=∠FGC,即可得到结论;
(2)在直角三角形EBF和直角三角形CFG中,利用勾股定理分别求出EF和FG的长度,再利用勾股定理求出EG的长度即可.
解答 解:(1)∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵EF⊥FG,
∴∠EFB+∠GFC=∠EFB+∠GFC=90°,
∴∠EFB=∠FGC,
∴△EBF∽△FCG;
(2)由(1)证得△EBF∽△FCG,
∴$\frac{BE}{CF}=\frac{BF}{CG}$,
∵F为BC的中点,
∴BF=CF,
∴$\frac{BE}{CF}=\frac{CF}{CG}$,
∴CF2=BE•CG=4,
∴CF=BF=2,BC=4,
∴EF2=BE2+BF2=5,FG2=CF2+CG2=20,
∵EF⊥FG,
∴EG2=EF2+FG2=25,
∴EG=5.
点评 本题考查了矩形的性质,勾股定理,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
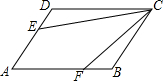 在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长为$\frac{9}{5}$.
在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长为$\frac{9}{5}$. 按照如图所示的操作步骤,若输入x的值为1,则输出的值为4.
按照如图所示的操作步骤,若输入x的值为1,则输出的值为4.