题目内容
8.若锐角α满足0°<α<45°,且sin2α=$\frac{\sqrt{3}}{2}$,则tanα=$\frac{\sqrt{3}}{3}$.分析 先根据60°的正弦值得到2α=60°,则α=30°,然后利用30度的正切值求解.
解答 解:∵sin2α=$\frac{\sqrt{3}}{2}$,
而0°<α<45°,
∴2α=60°,
∴α=30°
∴tanα=tan30°=$\frac{\sqrt{3}}{3}$.
故答案为$\frac{\sqrt{3}}{3}$.
点评 本题考查了特殊角的三角函数值:要熟记特殊角的三角函数值,可按值的变化规律去记,正弦逐渐增大,余弦逐渐减小,正切逐渐增大;也可按特殊直角三角形中各边特殊值规律去记.

练习册系列答案
相关题目
18.将二次函数y=x2-1的图象向右平移一个单位,向下平移2个单位得到( )
| A. | y=(x-1)2+1 | B. | y=(x+1)2+1 | C. | y=(x-1)2-3 | D. | y=(x+1)2+3 |
19.已知点A(-1,y1),B (2,y2)是反比例函数y=-$\frac{5}{x}$的图象上的两点,下列结论正确的是( )
| A. | y1<0<y2 | B. | y2<0<y1 | C. | y1<y2<0 | D. | y2<y1<0 |
13.已知m=n,下列等式不成立的是( )
| A. | 3m=3n | B. | $\frac{m}{4}$=$\frac{n}{4}$ | C. | -m+2=-n+2 | D. | m+1=n-1 |
 如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE=$\frac{1}{2}$.
如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE=$\frac{1}{2}$. 关于x的方程kx2+(3k+1)x+3=0.
关于x的方程kx2+(3k+1)x+3=0.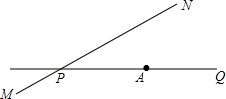 霾,也称阴霾、灰霾,是指原因不明的大量烟、尘等微粒悬浮而形成的浑浊现象.霾的核心物质是空气中悬浮的灰尘颗粒,气象学上称为气溶胶颗粒.随着中国社会的经济发展水平越来越高,越来越多的城市受雾霾影响.公路MN和公路PQ在点P处交汇,且∠QPN=30°,辰宇图象在点A处等公共汽车,AP=160m,一辆洒水车以3.6km/h的速度在公路MN上沿PN方向行驶,由于有霾,当时能见度只有100米,那么,辰宇同学能否会看到洒水车?如果不能看到,请说明理由;如果能看到,能看到几分钟?
霾,也称阴霾、灰霾,是指原因不明的大量烟、尘等微粒悬浮而形成的浑浊现象.霾的核心物质是空气中悬浮的灰尘颗粒,气象学上称为气溶胶颗粒.随着中国社会的经济发展水平越来越高,越来越多的城市受雾霾影响.公路MN和公路PQ在点P处交汇,且∠QPN=30°,辰宇图象在点A处等公共汽车,AP=160m,一辆洒水车以3.6km/h的速度在公路MN上沿PN方向行驶,由于有霾,当时能见度只有100米,那么,辰宇同学能否会看到洒水车?如果不能看到,请说明理由;如果能看到,能看到几分钟?