题目内容
3.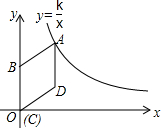 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点D的坐标为(4,3).
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点D的坐标为(4,3).(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=$\frac{k}{x}$(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
分析 (1)过点D作x轴的垂线,垂足为F,首先得出A点坐标,再利用反比例函数图象上点的坐标性质得出即可;
(2)将菱形ABCD沿x轴正方向平移,使得点D落在函数$y=\frac{32}{x}$(x>0)的图象D′点处,得出点D′的纵坐标为3,求出其横坐标,进而得出菱形ABCD平移的距离.
解答 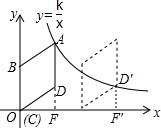 解:(1)过点D作x轴的垂线,垂足为F,
解:(1)过点D作x轴的垂线,垂足为F,
∵点D的坐标为(4,3),
∴OF=4,DF=3,
∴OD=5,
∴AD=5,
∴点A坐标为(4,8),
∴k=xy=4×8=32,
∴k=32;
(2)将菱形ABCD沿x轴正方向平移,使得点D落在函数$y=\frac{32}{x}$(x>0)的图象D′点处,
过点D′做x轴的垂线,垂足为F′.
∵DF=3,
∴D′F′=3,
∴点D′的纵坐标为3,
∵点D′在$y=\frac{32}{x}$的图象上
∴3=$\frac{32}{x}$,
解得:x=$\frac{32}{3}$,
即OF′=$\frac{32}{3}$,
∴FF′=$\frac{32}{3}$-4=$\frac{20}{3}$,
∴菱形ABCD平移的距离为$\frac{20}{3}$.
点评 此题主要考查了反比例函数综合以及反比例函数图象上点的坐标性质,得出A点坐标是解题关键.

练习册系列答案
相关题目
8.如图汽车标志中不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
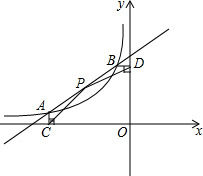 如图,A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y1=ax+b与反比例函数y2=$\frac{m}{x}$图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
如图,A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y1=ax+b与反比例函数y2=$\frac{m}{x}$图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D. 如图,已知在△ABC中,∠A=90°
如图,已知在△ABC中,∠A=90°
 如图,已知A(2$\sqrt{3}$,2)、B(2$\sqrt{3}$,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(-2,2$\sqrt{3}$)的位置,则图中阴影部分的面积为$\frac{3}{4}$π.
如图,已知A(2$\sqrt{3}$,2)、B(2$\sqrt{3}$,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(-2,2$\sqrt{3}$)的位置,则图中阴影部分的面积为$\frac{3}{4}$π.