题目内容
13. 如图,已知A(2$\sqrt{3}$,2)、B(2$\sqrt{3}$,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(-2,2$\sqrt{3}$)的位置,则图中阴影部分的面积为$\frac{3}{4}$π.
如图,已知A(2$\sqrt{3}$,2)、B(2$\sqrt{3}$,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(-2,2$\sqrt{3}$)的位置,则图中阴影部分的面积为$\frac{3}{4}$π.
分析 由A(2$\sqrt{3}$,2)使点A旋转到点A′(-2,2$\sqrt{3}$)的位置易得旋转90°,根据旋转的性质可得,阴影部分的面积等于S扇形A'OA-S扇形C'OC,从而根据A,B点坐标知OA=4,OC=OB=$\sqrt{13}$,可得出阴影部分的面积.
解答 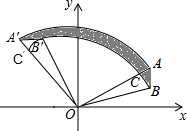 解:∵A(2$\sqrt{3}$,2)、B(2$\sqrt{3}$,1),
解:∵A(2$\sqrt{3}$,2)、B(2$\sqrt{3}$,1),
∴OA=4,OB=$\sqrt{13}$,
∵由A(2$\sqrt{3}$,2)使点A旋转到点A′(-2,2$\sqrt{3}$),
∴∠A′OA=∠B′OB=90°,
根据旋转的性质可得,S${\;}_{{OB}^{′}{C}^{′}}$=SOBC,
∴阴影部分的面积等于S扇形A'OA-S扇形C'OC=$\frac{1}{4}$π×42-$\frac{1}{4}$π×($\sqrt{13}$)2=$\frac{3}{4}π$,
故答案为:$\frac{3}{4}$π.
点评 此题主要考查了扇形的面积计算及旋转的性质,解答本题的关键是根据旋转的性质得出SOB′C′=SOBC,从而得到阴影部分的表达式.

练习册系列答案
相关题目
4.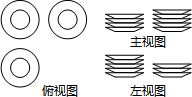 一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
 一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
1.3的相反数是( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
8. 已知二次函数y=ax2+bx+c的图象如图所示,记m=|a-b+c|+|2a+b+c|,n=|a+b+c|+|2a-b-c|.则下列选项正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,记m=|a-b+c|+|2a+b+c|,n=|a+b+c|+|2a-b-c|.则下列选项正确的是( )
 已知二次函数y=ax2+bx+c的图象如图所示,记m=|a-b+c|+|2a+b+c|,n=|a+b+c|+|2a-b-c|.则下列选项正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,记m=|a-b+c|+|2a+b+c|,n=|a+b+c|+|2a-b-c|.则下列选项正确的是( )| A. | m<n | B. | m>n | ||
| C. | m=n | D. | m、n的大小关系不能确定 |
18. 某班开展安全知识竞赛活动,班长将所有同学的成绩分成四类,并制作了如下的统计图表:
某班开展安全知识竞赛活动,班长将所有同学的成绩分成四类,并制作了如下的统计图表:
根据图表信息,回答下列问题:
(1)该班共有学生40人;表中a=20;
(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.
 某班开展安全知识竞赛活动,班长将所有同学的成绩分成四类,并制作了如下的统计图表:
某班开展安全知识竞赛活动,班长将所有同学的成绩分成四类,并制作了如下的统计图表:| 类别 | 成绩 | 频数 |
| 甲 | 60≤m<70 | 4 |
| 乙 | 70≤m<80 | a |
| 丙 | 80≤m<90 | 10 |
| 丁 | 90≤m≤100 | 6 |
(1)该班共有学生40人;表中a=20;
(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.
5.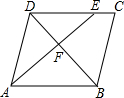 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )| A. | 3:4 | B. | 9:16 | C. | 9:1 | D. | 3:1 |
2.据2015年5月4日《天津日报》报道,“五一”三天假期,全市共接待海内外游客约2270000人次.将2270000用科学记数法表示应为( )
| A. | 0.227×lO7 | B. | 2.27×106 | C. | 22.7×l05 | D. | 227×104 |
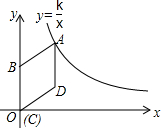 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点D的坐标为(4,3).
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点D的坐标为(4,3).