题目内容
9. 如图,AF∥CD,AB⊥BC,∠A=122°.
如图,AF∥CD,AB⊥BC,∠A=122°.(1)求∠C的度数;
(2)当∠F=∠C,∠E=81°,求∠D的度数;
(3)在(2)的条件下,求证:FE∥BC.
分析 (1)连接CF,由平行线的性质得到∠1=∠3,得到∠BCD=∠2+∠3=∠1+∠2,根据四边形的内角和即可得到结论;
(2)由∠F=∠C,得到∠1+∠4=∠3+∠4=148°,根据四边形的内角和即可得到结论;
(3)根据平行线的判定即可得到结论.
解答 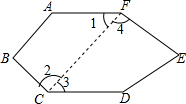 解:(1)连接CF,
解:(1)连接CF,
∵AF∥CD,
∴∠1=∠3,
∴∠BCD=∠2+∠3=∠1+∠2,
∵AB⊥BC,∠A=122°.
∴∠1+∠2=360°-∠A-∠B=148°,
∴∠BCD=148°;
(2)∵∠F=∠C,
∴∠1+∠4=∠3+∠4=148°,
∵∠E=81°,
∴∠D=360°-∠3-∠4-∠E=131°;
(3)∵∠AFE=∠BCD,∠1=∠3,
∴∠2=∠4,
∴EF∥BC.
点评 本题主要考查平行线的性质和判定,多边形内角和,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
 如图,⊙O的弦AB与CD相交于点E,若AE=6,BE=2,CE=3,则DE=4.
如图,⊙O的弦AB与CD相交于点E,若AE=6,BE=2,CE=3,则DE=4.
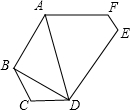 如图,六边形ABCDEF中,∠A=∠D,∠B=∠E,BC∥EF.
如图,六边形ABCDEF中,∠A=∠D,∠B=∠E,BC∥EF.