题目内容
15.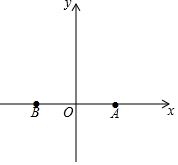 如图,在平面直角坐标系中,点A的坐标为(2,0),点A关于y轴的对称点为点B.
如图,在平面直角坐标系中,点A的坐标为(2,0),点A关于y轴的对称点为点B.(1)求点B的坐标;
(2)若以AB为一边向上作一个等边三角形ABC,求点C的坐标;
(3)求(2)中的三角形ABC的周长和面积.
分析 (1)A点(2,0)位于x轴上,且B点关于原点与A对称,故可得B的坐标为(-2,0);
(2)可知,O点为AB的中点,且△ABC为等边三角形,AB=24,根据三角函数关系,可得OC=2$\sqrt{3}$,即得C的坐标;
(3)由(1)、(2)得,AB=4,即得周长为12,而OC为高,故面积为4$\sqrt{3}$.
解答 解:(1)根据题意,A点关于原点的对称点为B,且A(2,0),
故B(-2,0);
(2)由(1)可得,AB=4,△ABC为等边三角形,
所以有OC=$\sqrt{3}$OA=2$\sqrt{3}$,
即C(0,2$\sqrt{3}$);
(3)由以上可知,AB=24,
故△ABC周长=12,
又OC=2$\sqrt{3}$,
即S△ABC=$\frac{1}{2}$×AB×OC=4$\sqrt{3}$.
点评 本题考查了等边三角形的性质,三角形的面积的计算,熟练掌握等边三角形的性质是解题的关键.

练习册系列答案
相关题目
6.平面直角坐标系中,⊙O是以原点O为圆心,4为半径的圆,则点A(2,-2)的位置在( )
| A. | ⊙O内 | B. | ⊙O上 | C. | ⊙O外 | D. | 不能确定 |
20.李华同学到文具店为学校美术组的40名学生购买铅笔和橡皮,已知铅笔每支m元,橡皮每个n元,若给每名同学买3支铅笔和5块橡皮,则一共需付款( )元.
| A. | 120m+5n | B. | 120m+200n | C. | 3m+5n | D. | 200m+120n |
5.下列有理数大小关系判断正确的是( )
| A. | -(-21)<+(-21) | B. | $-\frac{5}{6}<-\frac{4}{5}$ | C. | $-|{-10\frac{1}{2}}|>8\frac{2}{3}$ | D. | $-|{-7\frac{2}{3}}|=-(-7\frac{2}{3})$ |