题目内容
10.化简(1)$\sqrt{5}$-$\sqrt{\frac{1}{5}}$
(2)($\sqrt{2}$+1)2
(3)$\sqrt{5}$×$\sqrt{20}$-4
(4)$\frac{{\sqrt{27}-\sqrt{3}}}{{\sqrt{3}}}$+2
(5)$\sqrt{8}$+$\sqrt{18}$-$\sqrt{\frac{1}{2}}$
(6)($\sqrt{5}$-$\sqrt{7}$)($\sqrt{5}$+$\sqrt{7}$).
分析 (1)先把各二次根式化简为最简二次根式,然后合并即可;
(2)利用完全平方公式计算;
(3)根据二次根式的乘法法则运算;
(4)根据二次根式的除法法则运算;
(5)先把各二次根式化简为最简二次根式,然后合并即可;
(6)利用平方差公式计算.
解答 (1)解:原式═$\sqrt{5}-\frac{1}{5}\sqrt{5}=\frac{4}{5}\sqrt{5}$;
(2)解:原式=${(\sqrt{2})^2}+2\sqrt{2}+{1^2}=3+2\sqrt{2}+1=3+2\sqrt{2}$;
(3)解:原式=$\sqrt{5×20}-4=\sqrt{100}-4=10-4=6$;
(4)解:原式=$\frac{{\sqrt{27}}}{{\sqrt{3}}}-\frac{{\sqrt{3}}}{{\sqrt{3}}}+2=3-1+2=4$;
(5)解:原式=$2\sqrt{2}+3\sqrt{2}-\frac{1}{2}\sqrt{2}=\frac{9}{2}\sqrt{2}$;
(6)解:原式${(\sqrt{5})^2}-{(\sqrt{7})^2}=5-7=-2$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
相关题目
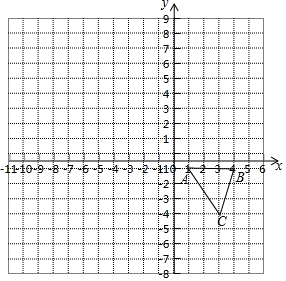 如图,△ABC顶点的坐标分别为A(1,-1),B(4,-1),C(3,-4).将△ABC绕点A逆时针旋转90°后,得到△AB1C1.在所给的直角坐标系中画出旋转后的△AB1C1,并直接写出点B1的坐标:
如图,△ABC顶点的坐标分别为A(1,-1),B(4,-1),C(3,-4).将△ABC绕点A逆时针旋转90°后,得到△AB1C1.在所给的直角坐标系中画出旋转后的△AB1C1,并直接写出点B1的坐标: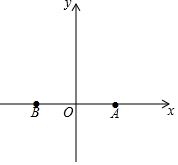 如图,在平面直角坐标系中,点A的坐标为(2,0),点A关于y轴的对称点为点B.
如图,在平面直角坐标系中,点A的坐标为(2,0),点A关于y轴的对称点为点B.