题目内容
5.下列有理数大小关系判断正确的是( )| A. | -(-21)<+(-21) | B. | $-\frac{5}{6}<-\frac{4}{5}$ | C. | $-|{-10\frac{1}{2}}|>8\frac{2}{3}$ | D. | $-|{-7\frac{2}{3}}|=-(-7\frac{2}{3})$ |
分析 分别根据正数与负数、负数与负数比较大小的法则进行比较即可.
解答 解:A、∵-(-21)=20>0,+(-21)=-20<0,∴-(-21)>+(-21),故本选项错误;
B、∵|-$\frac{5}{6}$|=$\frac{5}{6}$=$\frac{25}{30}$,|-$\frac{4}{5}$|=$\frac{4}{5}$=$\frac{24}{30}$$\frac{25}{30}$>$\frac{24}{30}$,∴-$\frac{5}{6}$<-$\frac{4}{5}$,故本选项正确;
C、∵-|-10$\frac{1}{2}$|=-10$\frac{1}{2}$<0,8$\frac{2}{3}$>0,∴、∵-|-10$\frac{1}{2}$|<8$\frac{2}{3}$,故本选项错误;
D、∵-|-7$\frac{2}{3}$|=-7$\frac{2}{3}$<0,-(-7$\frac{2}{3}$)=7$\frac{2}{3}$>0,∴-|-7$\frac{2}{3}$|<-(-7$\frac{2}{3}$),故本选项错误.
故选B.
点评 本题考查的是有理数的大小比较,熟知负数与负数比较大小的法则是解答此题的关键.

练习册系列答案
相关题目
10. 已知二次函数y=x2+2x-3.
已知二次函数y=x2+2x-3.
(1)把函数配成y=a(x-h)2+k的形式;
(2)求函数与x轴交点坐标;
(3)用五点法画函数图象
(4)当y>0时,则x的取值范围为x<-3或x>1.
(5)当-3<x<0时,则y的取值范围为-4≤y<0.
 已知二次函数y=x2+2x-3.
已知二次函数y=x2+2x-3.(1)把函数配成y=a(x-h)2+k的形式;
(2)求函数与x轴交点坐标;
(3)用五点法画函数图象
| x | … | … | |||||
| y | … | … |
(5)当-3<x<0时,则y的取值范围为-4≤y<0.
17.已知3x=5y(y≠0),那么下列比例式中正确的是( )
| A. | $\frac{x}{5}$=$\frac{y}{3}$ | B. | $\frac{x}{3}$=$\frac{y}{5}$ | C. | $\frac{x}{y}$=$\frac{3}{5}$ | D. | $\frac{x}{5}$=$\frac{3}{y}$ |
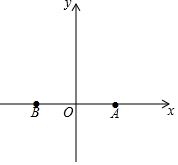 如图,在平面直角坐标系中,点A的坐标为(2,0),点A关于y轴的对称点为点B.
如图,在平面直角坐标系中,点A的坐标为(2,0),点A关于y轴的对称点为点B. 如图,将三角板与两边平行的直尺(EF∥HG)贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=55°,则∠1的度数等于35°.
如图,将三角板与两边平行的直尺(EF∥HG)贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=55°,则∠1的度数等于35°.