题目内容
19.先化简,再求值:$\frac{m-3}{3{m}^{2}-6m}$÷$(m+2-\frac{5}{m-2})$,其中m是方程x2+2x-3=0的根.分析 首先根据运算顺序和分式的化简方法,化简$\frac{m-3}{3{m}^{2}-6m}$÷$(m+2-\frac{5}{m-2})$,然后应用因数分解法解一元二次方程,求出m的值是多少;最后把求出的m的值代入化简后的算式,求出算式$\frac{m-3}{3{m}^{2}-6m}$÷$(m+2-\frac{5}{m-2})$的值是多少即可.
解答 解:$\frac{m-3}{3{m}^{2}-6m}$÷$(m+2-\frac{5}{m-2})$
=$\frac{m-3}{3m(m-2)}÷\frac{(m+3)(m-3)}{m-2}$
=$\frac{1}{3m(m+3)}$
∵x2+2x-3=0,
∴(x+3)(x-1)=0,
解得x1=-3,x2=1,
∵m是方程x2+2x-3=0的根,
∴m1=-3,m2=1,
∵m+3≠0,
∴m≠-3,
∴m=1,
所以原式=$\frac{1}{3m(m+3)}$
=$\frac{1}{3×1×(1+3)}$
=$\frac{1}{12}$
点评 (1)此题主要考查了分式的化简求值问题,注意化简时不能跨度太大,而缺少必要的步骤.
(2)此题还考查了解一元二次方程-因式分解法,要熟练掌握,解答此题的关键是要明确因式分解法解一元二次方程的一般步骤:①移项,使方程的右边化为零;②将方程的左边分解为两个一次因式的乘积;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就都是原方程的解.

练习册系列答案
相关题目
7. 如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=( )
如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=( )
 如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=( )
如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=( )| A. | 70° | B. | 80° | C. | 110° | D. | 100° |
4. 如图,AB∥CD,∠A=50°,则∠1的大小是( )
如图,AB∥CD,∠A=50°,则∠1的大小是( )
 如图,AB∥CD,∠A=50°,则∠1的大小是( )
如图,AB∥CD,∠A=50°,则∠1的大小是( )| A. | 50° | B. | 120° | C. | 130° | D. | 150° |
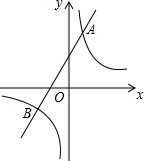 如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).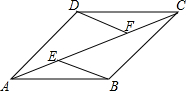 已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.
已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.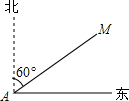 如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里.那么该船继续航行50$\sqrt{3}$海里可使渔船到达离灯塔距离最近的位置.
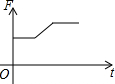
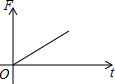
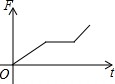
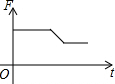
如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里.那么该船继续航行50$\sqrt{3}$海里可使渔船到达离灯塔距离最近的位置.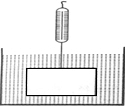 如图,挂在弹簧称上的长方体铁块浸没在水中,提着弹簧称匀速上移,直至铁块浮出水面停留在空中(不计空气阻力),弹簧称的读数F(kg)与时间t(s)的函数图象大致是( )
如图,挂在弹簧称上的长方体铁块浸没在水中,提着弹簧称匀速上移,直至铁块浮出水面停留在空中(不计空气阻力),弹簧称的读数F(kg)与时间t(s)的函数图象大致是( )