题目内容
16.(1)计算:$\frac{m}{m+1}+\frac{1}{m-1}-\frac{2}{{m}^{2}-1}$(2)先化简,再求值:(x-1-$\frac{8}{x+1}$)$÷\frac{x+3}{x+1}$,其中x=$\frac{2}{3}$.
分析 (1)先把后两项通分,再与第一项相加即可;
(2)先算括号里面的,再把除法变为乘法,约分即可,最后把x的值代入计算即可.
解答 解:(1)原式=$\frac{m}{m+1}$+$\frac{m+1}{(m+1)(m-1)}$-$\frac{2}{(m+1)(m-1)}$
=$\frac{m}{m+1}$+$\frac{1}{m+1}$
=1;
(2)原式=[$\frac{(x-1)(x+1)}{x+1}$-$\frac{8}{x+1}$]•$\frac{x+1}{x+3}$
=$\frac{{x}^{2}-9}{x+1}$•$\frac{x+1}{x+3}$
=$\frac{(x+3)(x-3)}{x+3}$
=x-3,
把x=$\frac{2}{3}$代入原式=$\frac{2}{3}$-3=-$\frac{7}{3}$.
点评 本题考查了分式的化简求值以及分式的混合运算,分式混合运算要注意先去括号;分子、分母能因式分解的先因式分解;除法要统一为乘法运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.抛物线y=(x+1)2-2的对称轴是( )
| A. | 直线x=1 | B. | 直线x=3 | C. | 直线x=-1 | D. | 直线x=-3 |
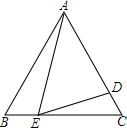 如图,等边三角形ABC的边长为5,点E为BC边上一点,且BE=2,点D为AC边上一点,若∠AED=60°,求CD的长?
如图,等边三角形ABC的边长为5,点E为BC边上一点,且BE=2,点D为AC边上一点,若∠AED=60°,求CD的长?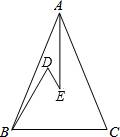 如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是8cm.
如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是8cm.