题目内容
如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=_____.

【答案】40°
【解析】试题分析:先根据三角形外角性质计算出∠EBF=∠A+∠E=85°,再根据圆内接四边形的性质计算出∠BCD=180°﹣∠A=125°,然后再根据三角形外角性质求∠F.
【解析】
∵∠A=55°,∠E=30°,
∴∠EBF=∠A+∠E=85°,
∵∠A+∠BCD=180°,
∴∠BCD=180°﹣55°=125°,
∵∠BCD=∠F+∠CBF,
∴∠F=125°﹣85°=40°.
故答案为40°.
考点:圆内接四边形的性质;三角形内角和定理.
【题型】填空题
【结束】
17
某果园有100棵橘子树,平均每一棵树结600个橘子.根据经验估计,每多种一棵树,平均每棵树就会少结5个橘子.设果园增种x棵橘子树,果园橘子总个数为y个,则果园里增种 棵橘子树,橘子总个数最多.
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目



 -24 B. 25π﹣24 C. 25π﹣12 D.
-24 B. 25π﹣24 C. 25π﹣12 D.  ,求线段OE的长.
,求线段OE的长.
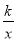 (k>0)的图象上,且x1=-x2,则( )
(k>0)的图象上,且x1=-x2,则( )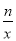 (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6. 的解集.
的解集.
 ;(2)(5,﹣4);(3)﹣2≤x<0或x≥5.
;(2)(5,﹣4);(3)﹣2≤x<0或x≥5.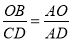 ,∴
,∴ ,∴CD=10,∴点C坐标(﹣2,10),B(0,6),A(3,0),∴
,∴CD=10,∴点C坐标(﹣2,10),B(0,6),A(3,0),∴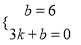 解得:
解得:  ,∴一次函数为y=﹣2x+6.
,∴一次函数为y=﹣2x+6.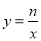 经过点C(﹣2,10),∴n=﹣20,∴反比例函数解析式为
经过点C(﹣2,10),∴n=﹣20,∴反比例函数解析式为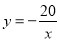 ;
; ,解得
,解得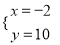 或
或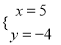 ,故另一个交点坐标为(5,﹣4);
,故另一个交点坐标为(5,﹣4);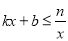 的解集:﹣2≤x<0或x≥5.
的解集:﹣2≤x<0或x≥5.


 , 其中x满足
, 其中x满足
