题目内容
 如图,等腰Rt△ABC中,AC=BC,∠ACB=90°,∠A、∠B、∠C的平分线交于点P.
如图,等腰Rt△ABC中,AC=BC,∠ACB=90°,∠A、∠B、∠C的平分线交于点P.(1)求证:AB=CP+BC;
(2)若∠A、∠B的外角平分线以及∠C的平分线交于点P,
①(1)中的结论是否成立?
②请画出图形,写出结论并证明.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)根据三角形的内角和定理,得出∠PAB+∠PBA=45°,∠PCB+∠PBC=67.5°,即可求出∠APB=135°,∠BPC=112.5°,作辅助线在AB上截取BG=BC,可证出△PBC≌△PBG(SAS),即可得出∠BPC=∠BPG=112.5°,PC=PG,BC=BG,再可证出∠APG=∠APB-∠BPG=22.5°,得出∠PAG=∠APG,进而得出AG=PG,即可得出AB=CP+BC.
(2)①(1)中的结论不成立;②延长AB至G,使BG=BC,先证得∠ACG=∠CBP112.5°,∠CAB=∠PCB=45°,然后根据ASA证得△GAC≌△PCB,即可证得PC=AB+BC.
(2)①(1)中的结论不成立;②延长AB至G,使BG=BC,先证得∠ACG=∠CBP112.5°,∠CAB=∠PCB=45°,然后根据ASA证得△GAC≌△PCB,即可证得PC=AB+BC.
解答: (1)证明:在AB上截取BG=BC,
(1)证明:在AB上截取BG=BC,
∵等腰Rt△ABC中,AC=BC,∠ACB=90°,
∴∠BAC=∠ABC=45°,
∵∠A、∠B、∠C的平分线交于点P.
∴∠PAB=∠PBA=22.5°,∠ACP=∠BCP=45°,
∴∠PAB+∠PBA=45°,∠PCB+∠PBC=67.5°
∴∠APB=135°,∠BPC=112.5°,
在△PBC和△PBG中,
,
∴△PBC≌△PBG(SAS),
∴∠BPC=∠BPG=112.5°,PC=PG,BC=BG,
∴∠APG=∠APB-∠BPG=22.5°,
∴∠PAG=∠APG,
∴AG=PG,
∴AG=PC,
∴AB=BG+AG=CP+BC,
即AB=CP+BC;
(2)①(1)中的结论不成立;
②如图2所示,PC= AB+BC;
AB+BC;
证明:延长AB至G,使BG=BC,
∴∠BCG=∠BGC,
∵∠CAB=∠ABC=45°,
∴∠CBG=135°,
∴∠BCG=∠BGC=22.5°,
∴∠ACG=112,5°,
∵∠A、∠B的外角平分线以及∠C的平分线交于点P,
∴∠PCB=45°,∠PBC=112.5°,
∴∠ACG=∠CBP,∠CAB=∠PCB=45°,
在△GAC和△PCB中,
,
∴△GAC≌△PCB(ASA),
∴AG=PC,
∴PC=AB+BG=AB+BC,
即PC=AB+BC.
 (1)证明:在AB上截取BG=BC,
(1)证明:在AB上截取BG=BC,∵等腰Rt△ABC中,AC=BC,∠ACB=90°,
∴∠BAC=∠ABC=45°,
∵∠A、∠B、∠C的平分线交于点P.
∴∠PAB=∠PBA=22.5°,∠ACP=∠BCP=45°,
∴∠PAB+∠PBA=45°,∠PCB+∠PBC=67.5°
∴∠APB=135°,∠BPC=112.5°,
在△PBC和△PBG中,
|
∴△PBC≌△PBG(SAS),
∴∠BPC=∠BPG=112.5°,PC=PG,BC=BG,
∴∠APG=∠APB-∠BPG=22.5°,
∴∠PAG=∠APG,
∴AG=PG,
∴AG=PC,
∴AB=BG+AG=CP+BC,
即AB=CP+BC;
(2)①(1)中的结论不成立;
②如图2所示,PC=
 AB+BC;
AB+BC;证明:延长AB至G,使BG=BC,
∴∠BCG=∠BGC,
∵∠CAB=∠ABC=45°,
∴∠CBG=135°,
∴∠BCG=∠BGC=22.5°,
∴∠ACG=112,5°,
∵∠A、∠B的外角平分线以及∠C的平分线交于点P,
∴∠PCB=45°,∠PBC=112.5°,
∴∠ACG=∠CBP,∠CAB=∠PCB=45°,
在△GAC和△PCB中,
|
∴△GAC≌△PCB(ASA),
∴AG=PC,
∴PC=AB+BG=AB+BC,
即PC=AB+BC.
点评:本题考查了等腰直角三角形的性质,全等三角形的判定和性质,作出辅助线构建全等三角形是本题的关键.

练习册系列答案
相关题目
 如图,△ABC是⊙O的内接等边三角形,⊙O的半径为r.
如图,△ABC是⊙O的内接等边三角形,⊙O的半径为r.
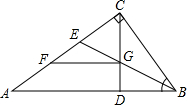 如图,已知△ABC中,∠ACB=90°,CD⊥AB于D,∠ABC的角平分线BE交CD于G,交AC于E,GF∥AB交AC于F.求证:AF=CG.
如图,已知△ABC中,∠ACB=90°,CD⊥AB于D,∠ABC的角平分线BE交CD于G,交AC于E,GF∥AB交AC于F.求证:AF=CG.