题目内容
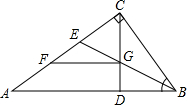 如图,已知△ABC中,∠ACB=90°,CD⊥AB于D,∠ABC的角平分线BE交CD于G,交AC于E,GF∥AB交AC于F.求证:AF=CG.
如图,已知△ABC中,∠ACB=90°,CD⊥AB于D,∠ABC的角平分线BE交CD于G,交AC于E,GF∥AB交AC于F.求证:AF=CG.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:分别过G、F作GH⊥BC,FI⊥AB,垂足分别为H、I,由条件证明△AFI≌△CGH即可.
解答: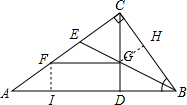 证明:分别过G、F作GH⊥BC,FI⊥AB,垂足分别为H、I,
证明:分别过G、F作GH⊥BC,FI⊥AB,垂足分别为H、I,
∵CD⊥AB于D,GF∥AB,
∴四边形DGFI为矩形,
∴FI=GD,
∵BE平分∠ABC,
∴GD=GH,
∴FI=GH,
∵∠ACB=90°,
∴∠DCH+∠ACD=90°,
且∠A+∠ACD=90°,
∴∠FAI=∠GCH,
在△AFI和△CGH中,
,
∴△AFI≌△CGH(AAS),
∴AF=CG.
 证明:分别过G、F作GH⊥BC,FI⊥AB,垂足分别为H、I,
证明:分别过G、F作GH⊥BC,FI⊥AB,垂足分别为H、I,∵CD⊥AB于D,GF∥AB,
∴四边形DGFI为矩形,
∴FI=GD,
∵BE平分∠ABC,
∴GD=GH,
∴FI=GH,
∵∠ACB=90°,
∴∠DCH+∠ACD=90°,
且∠A+∠ACD=90°,
∴∠FAI=∠GCH,
在△AFI和△CGH中,
|
∴△AFI≌△CGH(AAS),
∴AF=CG.
点评:本题主要考查三角形全等判定和性质,分别过G、F作GH⊥BC,FI⊥AB,构造出全等三角形是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
32010的个位数字为( )
| A、1 | B、3 | C、9 | D、7 |
 如图,等腰Rt△ABC中,AC=BC,∠ACB=90°,∠A、∠B、∠C的平分线交于点P.
如图,等腰Rt△ABC中,AC=BC,∠ACB=90°,∠A、∠B、∠C的平分线交于点P. 看图填空:
看图填空: