题目内容
7.已知关于x的方程$\frac{1}{4}$x2-(m-2)x+m2=0的两根为x1,x2(1)求m的取值范围;
(2)当x12-x22=0时,求m的值.
分析 (1)若一元二次方程有两实数根,则根的判别式△=b2-4ac≥0,建立关于m的不等式,求出m的取值范围;
(2)由x12-x22=0得x1+x2=0或x1-x2=0;当x1+x2=0时,运用两根关系可以得到4(m-2)=0或方程有两个相等的实根,据此即可求得m的值.
解答 解:(1)由题意有△=[-(m-2)]2-4×$\frac{1}{4}$m2≥0,
解得m≤1,
所以实数m的取值范围是m≤1;
(2)由两根关系,得根x1+x2=4(m-2),x1•x2=4m2,
由x12-x22=0得(x1+x2)(x1-x2)=0,
若x1+x2=0,即4(m-2)=0,解得m=2,
∵m≤1,
∴m=2不合题意,舍去,
若x1-x2=0,即x1=x2,
∴△=0,由(1)知m=1,
故当x12-x22=0时,m=1.
点评 本题考查了一元二次方程根的判别式及根与系数的关系,利用两根关系得出的结果必须满足△≥0的条件.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
12.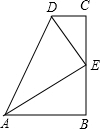 在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有( )个.
在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有( )个.
(1)AE平分∠DAB;(2)△EBA≌△DCE;(3)AB+CD=AD;(4)AE⊥DE;(5)AB∥CD.
 在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有( )个.
在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有( )个.(1)AE平分∠DAB;(2)△EBA≌△DCE;(3)AB+CD=AD;(4)AE⊥DE;(5)AB∥CD.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
19.关于函数y=-3(x+4)2+2,下列叙述正确的是( )
| A. | 它的图象是一条关于直线x=4对称的抛物线 | |
| B. | 这个函数有最小值是2 | |
| C. | 当x<0时,y随着x的增大而增大 | |
| D. | 当x<-4时,y随着x的增大而增大 |
 阅读下列材料,并解决后面的问题.
阅读下列材料,并解决后面的问题.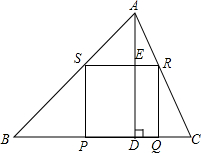 如图,AD是△ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=30cm,AD=20cm,四边形PQRS是正方形.
如图,AD是△ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=30cm,AD=20cm,四边形PQRS是正方形.