题目内容
18. 如图,某栋楼顶部有一信号发射塔,在矩形建筑物ABCD的D、C两点处测得该塔顶端F的仰角分别为∠α=30°、∠β=60°,矩形建筑物高度DC=30m.计算该信号发射塔顶端到地面的高度FG.
如图,某栋楼顶部有一信号发射塔,在矩形建筑物ABCD的D、C两点处测得该塔顶端F的仰角分别为∠α=30°、∠β=60°,矩形建筑物高度DC=30m.计算该信号发射塔顶端到地面的高度FG.
分析 延长AD交FG于点E,在Rt△FDE中,根据tanα=$\frac{FE}{DE}$,tanβ=$\frac{FG}{CG}$,得到FG=FE+EG,列方程解答即可.
解答  解:如图,延长AD交FG于点E.
解:如图,延长AD交FG于点E.
设DE=x,由题意得EG=DC=30,CG=DE=x.
在Rt△FDE中,tanα=$\frac{FE}{DE}$,
∴FE=DE•tanα=$\frac{\sqrt{3}}{3}$x,
在Rt△FCG中,tanβ=$\frac{FG}{CG}$,
∴FG=CG•tanβ=$\sqrt{3}$x,
∵FG=FE+EG,
∴$\sqrt{3}$x=$\frac{\sqrt{3}}{3}$x+30,
解得,x=15$\sqrt{3}$,
FG=45m.
答:该信号塔发射顶端到地面的高度FG为45m.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
8.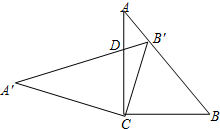 在Rt△ABC中,∠C=90°,cosB=$\frac{3}{5}$,把这个直角三角形绕顶点C旋转后得到Rt△A′B′C,其中点B′正好落在AB上,A′B′与AC相交于点D,那么$\frac{B′D}{CD}$等于( )
在Rt△ABC中,∠C=90°,cosB=$\frac{3}{5}$,把这个直角三角形绕顶点C旋转后得到Rt△A′B′C,其中点B′正好落在AB上,A′B′与AC相交于点D,那么$\frac{B′D}{CD}$等于( )
 在Rt△ABC中,∠C=90°,cosB=$\frac{3}{5}$,把这个直角三角形绕顶点C旋转后得到Rt△A′B′C,其中点B′正好落在AB上,A′B′与AC相交于点D,那么$\frac{B′D}{CD}$等于( )
在Rt△ABC中,∠C=90°,cosB=$\frac{3}{5}$,把这个直角三角形绕顶点C旋转后得到Rt△A′B′C,其中点B′正好落在AB上,A′B′与AC相交于点D,那么$\frac{B′D}{CD}$等于( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{7}{20}$ |
7.若1<x<3,则|x-3|+$\sqrt{(x-1)^{2}}$的值为( )
| A. | 2x-4 | B. | -2 | C. | 4-2x | D. | 2 |
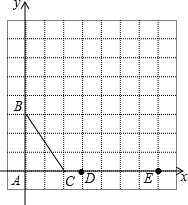 如图,在方格纸中,以每个小方格的边长为单位1,△ABC和△EPD的顶点均在格点上,请你提供一个符合条件的点P,使△ABC与以E、P、D为顶点的三角形相似,则点P所在的格点坐标可以是(3,6).
如图,在方格纸中,以每个小方格的边长为单位1,△ABC和△EPD的顶点均在格点上,请你提供一个符合条件的点P,使△ABC与以E、P、D为顶点的三角形相似,则点P所在的格点坐标可以是(3,6).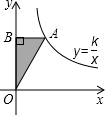 如图,在平面直角坐标系中,已知点A是反比例函数的图象y=$\frac{k}{x}$(k≠0)的图象上一点,AB⊥y轴于B,且△AOB的面积为3,则k的值是( )
如图,在平面直角坐标系中,已知点A是反比例函数的图象y=$\frac{k}{x}$(k≠0)的图象上一点,AB⊥y轴于B,且△AOB的面积为3,则k的值是( ) 将正整数按如图所示的规律排列下去.若用有序实数对(m,n)表示第m排、从左到右第n个数,如(3,2)表示实数5.
将正整数按如图所示的规律排列下去.若用有序实数对(m,n)表示第m排、从左到右第n个数,如(3,2)表示实数5. 如图,已知AB∥CD,∠2=120°,则∠1的度数是为60°.
如图,已知AB∥CD,∠2=120°,则∠1的度数是为60°.