题目内容
9.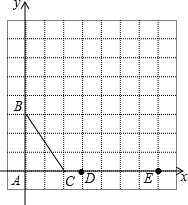 如图,在方格纸中,以每个小方格的边长为单位1,△ABC和△EPD的顶点均在格点上,请你提供一个符合条件的点P,使△ABC与以E、P、D为顶点的三角形相似,则点P所在的格点坐标可以是(3,6).
如图,在方格纸中,以每个小方格的边长为单位1,△ABC和△EPD的顶点均在格点上,请你提供一个符合条件的点P,使△ABC与以E、P、D为顶点的三角形相似,则点P所在的格点坐标可以是(3,6).
分析 利用∠PDE=90°,$\frac{PD}{AB}$=$\frac{DE}{AC}$可判断△PDE∽△BAC,根据相似比计算出PD,从而得到一个符合条件的点P的坐标.
解答 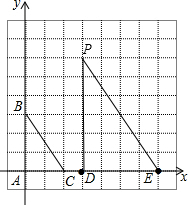 解:AB=3,AC=4,∠BAC=90°,DE=4,
解:AB=3,AC=4,∠BAC=90°,DE=4,
若∠PDE=90°,$\frac{PD}{AB}$=$\frac{DE}{AC}$时,△PDE∽△BAC,即$\frac{PD}{3}$=$\frac{4}{2}$,解得PD=6,
此时P点坐标为(3,6),
所以当点P坐标为(3,6)时,使△ABC与以E、P、D为顶点的三角形相似.
故答案为(3,6).
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.也考查了坐标与图形性质.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
14.下列四个几何体中,主视图与其它三个不同的是( )
| A. |  | B. |  | C. |  | D. |  |
1.3的平方根是( )
| A. | 3 | B. | ±3 | C. | $\sqrt{3}$ | D. | ±$\sqrt{3}$ |
19.下列交通标志中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
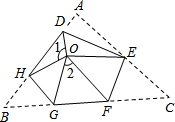 如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为180°.
如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为180°. 如图,某栋楼顶部有一信号发射塔,在矩形建筑物ABCD的D、C两点处测得该塔顶端F的仰角分别为∠α=30°、∠β=60°,矩形建筑物高度DC=30m.计算该信号发射塔顶端到地面的高度FG.
如图,某栋楼顶部有一信号发射塔,在矩形建筑物ABCD的D、C两点处测得该塔顶端F的仰角分别为∠α=30°、∠β=60°,矩形建筑物高度DC=30m.计算该信号发射塔顶端到地面的高度FG.