题目内容
8.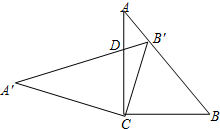 在Rt△ABC中,∠C=90°,cosB=$\frac{3}{5}$,把这个直角三角形绕顶点C旋转后得到Rt△A′B′C,其中点B′正好落在AB上,A′B′与AC相交于点D,那么$\frac{B′D}{CD}$等于( )
在Rt△ABC中,∠C=90°,cosB=$\frac{3}{5}$,把这个直角三角形绕顶点C旋转后得到Rt△A′B′C,其中点B′正好落在AB上,A′B′与AC相交于点D,那么$\frac{B′D}{CD}$等于( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{7}{20}$ |
分析 如图,作辅助线;首先求出BM的长度,进而求出AC、BB′的长度;证明△A′DC∽△ADB′,得$\frac{B′D}{CD}=\frac{AB′}{A′C}$=$\frac{7}{20}$,即可解决问题.
解答 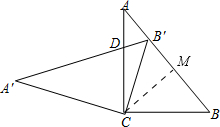 解:如图,过点C作CM⊥AB于点M,
解:如图,过点C作CM⊥AB于点M,
∵∠C=90°,cosB=$\frac{3}{5}$,
∴$\frac{BC}{AB}=\frac{3}{5}$;设BC=3λ,则AB=5λ,
由勾股定理得AC=4λ,
由射影定理得:BC2=BM•AB,
∴BM=$\frac{9}{5}λ$.由旋转变换的性质得:
CB=CB′,A′C=AC=4λ,∠A′=∠A;而CM⊥BB′,
∴B′M=BM,AB′=5λ-$\frac{18}{5}λ$=$\frac{7}{5}λ$,
∵∠A′=∠A,∠A′DC=∠ADB′,
∴△A′DC∽△ADB′,
∴$\frac{B′D}{CD}=\frac{AB′}{A′C}$=$\frac{7}{20}$,
故选D.
点评 该题主要考查了旋转变换的性质、勾股定理、相似三角形的判定等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用旋转变换的性质、勾股定理等几何知识点来分析、判断、推理或解答.

练习册系列答案
相关题目
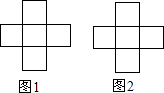 如图,由5个边长为1的正方形组成一个“十”字形,一共有12个顶点,要求:从这12点中取出4个点,直接在图中连出不同大小的正方形,并写出相应的正方形的边长.
如图,由5个边长为1的正方形组成一个“十”字形,一共有12个顶点,要求:从这12点中取出4个点,直接在图中连出不同大小的正方形,并写出相应的正方形的边长.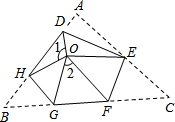 如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为180°.
如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为180°.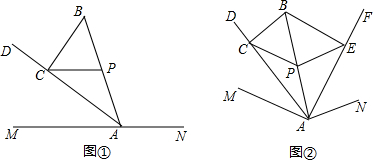
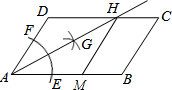 如图,在平行四边形ABCD中,AB>AD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H;过点H作HM∥BC交AB于M.则下列结论:①AG平分∠DAB,②S△ADH=$\frac{1}{2}$S四边形ABCH,③△ADH是等腰三角形,④四边形ADHM为菱形.其中正确的是①③④.
如图,在平行四边形ABCD中,AB>AD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H;过点H作HM∥BC交AB于M.则下列结论:①AG平分∠DAB,②S△ADH=$\frac{1}{2}$S四边形ABCH,③△ADH是等腰三角形,④四边形ADHM为菱形.其中正确的是①③④. 如图,某栋楼顶部有一信号发射塔,在矩形建筑物ABCD的D、C两点处测得该塔顶端F的仰角分别为∠α=30°、∠β=60°,矩形建筑物高度DC=30m.计算该信号发射塔顶端到地面的高度FG.
如图,某栋楼顶部有一信号发射塔,在矩形建筑物ABCD的D、C两点处测得该塔顶端F的仰角分别为∠α=30°、∠β=60°,矩形建筑物高度DC=30m.计算该信号发射塔顶端到地面的高度FG.