题目内容
6. 如图,小正方形的边长为1,则图中三角形(阴影部分)与△ABC相似的是( )
如图,小正方形的边长为1,则图中三角形(阴影部分)与△ABC相似的是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据网格中的数据求出AB,AC,BC的长,求出三边之比,利用三边对应成比例的两三角形相似判断即可.
解答 解:根据题意得:AC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,AB=2,BC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,∴BC:AB:AC=1:$\sqrt{2}$:$\sqrt{5}$,
A、三边之比为1:$\sqrt{5}$:2$\sqrt{2}$,图中的三角形(阴影部分)与△ABC不相似;
B、三边之比为1:$\sqrt{2}$:$\sqrt{5}$,图中的三角形(阴影部分)与△ABC相似;
C、三边之比为$\sqrt{2}$:$\sqrt{5}$:3,图中的三角形(阴影部分)与△ABC不相似;
D、三边之比为2:$\sqrt{5}$:$\sqrt{13}$,图中的三角形(阴影部分)与△ABC不相似.
故选B.
点评 此题考查了相似三角形的判定,熟练掌握相似三角形的判定方法是解本题的关键.

练习册系列答案
相关题目
14.已知单项式4x3ym与-3xn-1y3的和是单项式,则这两个单项式的和是( )
| A. | x2y3 | B. | x3y2 | C. | xn-1ym | D. | xn+2ym+2 |
15.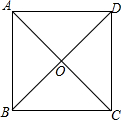 如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )
如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )
 如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )
如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )| A. | AO=BO=CO=DO,AC⊥BD | B. | AC=BC=CD=DA | ||
| C. | AO=CO,BO=DO,AC⊥BD | D. | AB=BC,CD⊥DA |
 已知:如图,△ABC是等边三角形,与BC平行的直线分别交AB和AC于点D,E,求证:△ADE是等边三角形.
已知:如图,△ABC是等边三角形,与BC平行的直线分别交AB和AC于点D,E,求证:△ADE是等边三角形. 如图:已知直线y1=-2x+3和直线y2=mx-1分别交y轴于点A、B,两直线交于点C(1,n).
如图:已知直线y1=-2x+3和直线y2=mx-1分别交y轴于点A、B,两直线交于点C(1,n).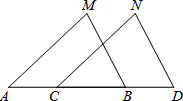 已知:点 A、C、B、D在同一条直线,∠M=∠N,AM=CN.请你添加一个条件,使△ABM≌△CDN,并给出证明.
已知:点 A、C、B、D在同一条直线,∠M=∠N,AM=CN.请你添加一个条件,使△ABM≌△CDN,并给出证明.