题目内容
13．$\left\{\begin{array}{l}{\frac{m}{3}-\frac{n}{4}=-1}\\{\frac{m}{2}+\frac{n}{3}=7}\end{array}\right.$．分析 方程组整理后，利用加减消元法求出解即可．
解答 解：方程组整理得：$\left\{\begin{array}{l}{4m-3n=-12①}\\{3m+2n=42②}\end{array}\right.$，
①×2+②×3得：17m=102，
解得：m=6，
把m=6代入②得：n=12，
则方程组的解为$\left\{\begin{array}{l}{m=6}\\{n=12}\end{array}\right.$．
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
7．
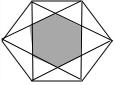如图，边长为a的正六边形中，连接一些顶点，中间围成一个新的小正六边形（阴影部分），则$\frac{{l}_{外部正六边形}}{{l}_{阴影}}$（l为周长）等于（ ）
如图，边长为a的正六边形中，连接一些顶点，中间围成一个新的小正六边形（阴影部分），则$\frac{{l}_{外部正六边形}}{{l}_{阴影}}$（l为周长）等于（ ）| A． | 3 | B． | $\sqrt{3}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | 2 |
8．以40m/s的速度将小球沿与地面成30°角的方向击出时，球的飞行路线将是一条抛物线．如果不考虑空气阻力，球的飞行高度h（米）与飞行时间t（秒）的关系如下表，且h与t的函数关系是我们学过的一次函数、二次函数、反比例函数中的一种
（1）请你从上述函数中选择一种合适的函数，求出它的函数关系式，并简要说明不选择另外两种函数的理由
（2）什么时候小球最高？最大高度是多少？
（3）小球运动的时间t在什么范围内，小球在运动过程中的高度不低于18.75米．
| 时间t（秒） | 0 | 1 | 3 | 4 |
| 高度h（米） | 0 | 15 | 15 | 0 |
（2）什么时候小球最高？最大高度是多少？
（3）小球运动的时间t在什么范围内，小球在运动过程中的高度不低于18.75米．
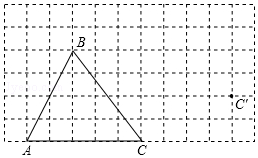画图并填空：