题目内容
5．某体育用品商场为推销某一品牌运动服，先做了市场调查，发现卖出价为50元/件时，月销售量为500件，每提价1元，月销售量减少10件．若该运动服的买入价为40元/件，请解答下列问题：（1）试求月销售利润y（元）与卖出价格x（元/件）的函数关系式；
（2）当卖出价格为多少时，能获得最大月利润，最大月利润是多少？
分析 （1）根据题意得出月销售量为500-10（x-50），每件利润为（x-40）元，即可得出月销售利润y（元）与卖出价格x（元/件）的函数关系式；
（2）y是x的二次函数，-10＜0，y有最大值，化成顶点式，即可得出结果．
解答 解：（1）根据题意得：y=（x-40）[500-10（x-50）]=-10x2+1400x-40000，
∴y=-10x2+1400x-40000；
（2）∵y=-10x2+1400x-40000=-10（x-70）2+9000，
又∵-10＜0，
∴y有最大值，
当x=70时，y最大=9000；
∴当卖出价格为70元时，能获得最大月利润，最大月利润为9000元．
点评 本题考查了二次函数的解析式的确定以及运用；根据题意得出y与x的函数关系式是解决问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．下列运算正确的是（ ）
| A． | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B． | $\sqrt{2}•\sqrt{3}=\sqrt{6}$ | C． | a6÷a2=a3 | D． | $\sqrt{（-2}{）^2}=-2$ |
如图，在△ABC中，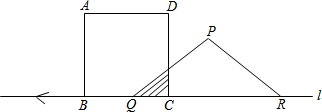
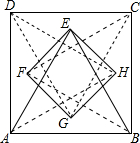如图，分别以正方形ABCD的四条边为边，向其内部作等边三角形，得到△ABE、△BCF、△CDG、△DAH，连接EF、FG、GH、HE，若AB=2，则四边形EFGH的面积为8-4$\sqrt{3}$．
如图，这是一个供滑板爱好者使用的U型池，该U型池可以看作是一个长方体去掉一个“半圆柱”而成，中间可供滑行部分的截面是半径为4m的半圆，其边缘AB=CD=18m，点E在CD上，CE=2cm，一滑行爱好者从A点到E点，再从E点滑行到B点，则他滑行的最短距离是多少？（边缘部分的厚度可以忽略不计，π取3）