题目内容
 已知,如图,四边形ABCD四条边上的中点分别为E,F,G,H,顺次连接EF,FG,GH,HE,得到四边形EFGH(即四边形ABCD的中点四边形).
已知,如图,四边形ABCD四条边上的中点分别为E,F,G,H,顺次连接EF,FG,GH,HE,得到四边形EFGH(即四边形ABCD的中点四边形).(1)四边形EFGH的形状是
(2)连接四边形ABCD的对角线AC与BD,当AC与BD满足
考点:中点四边形
专题:
分析:(1)连接BD,根据三角形的中位线定理得到EH∥BD,EH=
BD,FG∥BD,FG=
BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
(2)根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形;
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形;
解答:解:(1)四边形EFGH的形状是平行四边形.理由如下:
如图,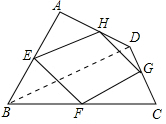 连结BD.
连结BD.
∵E、H分别是AB、AD中点,
∴EH∥BD,EH=
BD,
同理FG∥BD,FG=
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.理由如下:
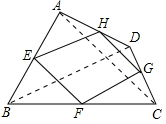 如图,连结AC、BD.
如图,连结AC、BD.
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;
故答案为:平行四边形,对角线满足互相垂直.
如图,
 连结BD.
连结BD.∵E、H分别是AB、AD中点,
∴EH∥BD,EH=
| 1 |
| 2 |
同理FG∥BD,FG=
| 1 |
| 2 |
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.理由如下:
 如图,连结AC、BD.
如图,连结AC、BD.∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;
故答案为:平行四边形,对角线满足互相垂直.
点评:本题主要考查对三角形的中位线定理,平行四边形的判定,矩形的判定等知识点的理解和掌握,熟练掌握各定理是解决此题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 如图,矩形ABCD中,AB=3,AD=5,点E在AD上,且AE:ED=1:4,联结BE,射线EF⊥BE交边DC于点F.求CF的长.
如图,矩形ABCD中,AB=3,AD=5,点E在AD上,且AE:ED=1:4,联结BE,射线EF⊥BE交边DC于点F.求CF的长. △ABC是⊙O的内接三角形,∠BAC=60°,AB=10,AC=6,AM平分∠BAC,且与⊙O相交于点M,过点M作直线DE,使DE∥BC.
△ABC是⊙O的内接三角形,∠BAC=60°,AB=10,AC=6,AM平分∠BAC,且与⊙O相交于点M,过点M作直线DE,使DE∥BC. 如图,在菱形ABCD中,AB=2,∠B=60°.将一个60°的∠PCQ的顶点放在点C处,并绕点C旋转,当CP与AB交于点M,CQ同时与AD交于点N时.
如图,在菱形ABCD中,AB=2,∠B=60°.将一个60°的∠PCQ的顶点放在点C处,并绕点C旋转,当CP与AB交于点M,CQ同时与AD交于点N时. 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=