题目内容
 如图所示,已知边长为12的正方形ABCD中,E是CD上一点,DE=5,AE的中垂线分别交AD,BC于点M,N,垂足为P点,则
如图所示,已知边长为12的正方形ABCD中,E是CD上一点,DE=5,AE的中垂线分别交AD,BC于点M,N,垂足为P点,则| PM |
| MN |
考点:正方形的性质,全等三角形的判定与性质,线段垂直平分线的性质,相似三角形的判定与性质
专题:
分析:由勾股定理求AE的长,过M点作MG⊥BC,垂足为G,利用互余关系证明∠DAE=∠GMN,可证△DAE≌△GMN,从而有MN=AE,从而求得MN的长.然后根据三角形相似求得PM的长,即可求得
的值.
| PM |
| MN |
解答: 解:∵正方形ABCD的边长为12,点E在BC上,DE=5,
解:∵正方形ABCD的边长为12,点E在BC上,DE=5,
∴AE=
=
=13,
过M点作MG⊥BC,垂足为G,
∴四边形MDCG是矩形,
∴MG=DC,
∴MG=AD,
∵∠DAE+∠AMN=90°,∠GMN+∠AMN=90°,
∴∠DAE=∠GMN,
在△DAE与△GMN中,
,
∴DAEP≌△GMN(ASA),
∴MN=AE=13,
∵AE=13,
∴AP=
,
∵∠D=∠APM=90°,
∴∠AMN=∠AED,
∴△AMP∽△AED,
∴
=
,
即
=
,解得PM=
,
∴
=
=
.
故答案为
.
 解:∵正方形ABCD的边长为12,点E在BC上,DE=5,
解:∵正方形ABCD的边长为12,点E在BC上,DE=5,∴AE=
| AD2+DE2 |
| 122+52 |
过M点作MG⊥BC,垂足为G,
∴四边形MDCG是矩形,
∴MG=DC,
∴MG=AD,
∵∠DAE+∠AMN=90°,∠GMN+∠AMN=90°,
∴∠DAE=∠GMN,
在△DAE与△GMN中,
|
∴DAEP≌△GMN(ASA),
∴MN=AE=13,
∵AE=13,
∴AP=
| 13 |
| 2 |
∵∠D=∠APM=90°,
∴∠AMN=∠AED,
∴△AMP∽△AED,
∴
| PM |
| DE |
| AP |
| AD |
即
| PM |
| 5 |
| ||
| 12 |
| 65 |
| 24 |
∴
| PM |
| MN |
| ||
| 13 |
| 5 |
| 24 |
故答案为
| 5 |
| 24 |
点评:本题考查了全等三角形的判断与性质,正方形的性质、勾股定理的运用以及三角形相似的判定和性质,作辅助线,构造全等三角形是本题的关键.

练习册系列答案
相关题目
如图所示,经过折叠能围成一个正方体的是( )
A、 |
B、 |
C、 |
D、 |
若正多边形面积是100,周长是40,则它的边心距是( )
| A、5 | B、2.5 | C、10 | D、20 |
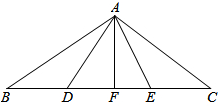 如图,点D,E在△ABC的边BC上,现有3个语句:①AB=AC;②AD=AE;③BD=CE.
如图,点D,E在△ABC的边BC上,现有3个语句:①AB=AC;②AD=AE;③BD=CE.