题目内容
4.若关于t的不等式组$\left\{\begin{array}{l}{t-a≥0}\\{2t+1≤4}\end{array}\right.$,恰有三个整数解,试化简,求式子|a+2|+|-a-1|的值.分析 首先解不等式组中的每个不等式,根据不等式组只有三个整数解确定a的整数值即可求得a的范围,进而化简即可.
解答 解:由①得:t≥a,
由②得:x≤$\frac{3}{2}$,
不等式组的解集为a≤t≤$\frac{3}{2}$,
若不等式组恰有三个整数解,则一定是-1,0,1.
所以-2<a≤-1.
|a+2|+|-a-1|=a+2-a-1=1.
点评 此题考查的是一元一次不等式的解法,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
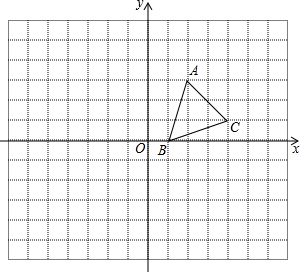 如图,方格纸中的每个小方格都是边长为1单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
如图,方格纸中的每个小方格都是边长为1单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
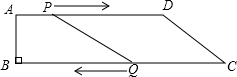 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=9cm,BC=13cm.点P从点A出发,以1cm/s的速度向终点D运动;点Q从点C同时出发,以2cm/s的速度向终点B运动,当其中一个动点到达终点时,另一个点也随之停止运动.设运动时间为ts.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=9cm,BC=13cm.点P从点A出发,以1cm/s的速度向终点D运动;点Q从点C同时出发,以2cm/s的速度向终点B运动,当其中一个动点到达终点时,另一个点也随之停止运动.设运动时间为ts.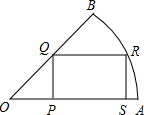 如图,扇形中∠AOB=45°,半径OB=2,矩形PQRS的顶点P、S在半径OA上,Q在半径OB上,R在弧AB上,连接OR.
如图,扇形中∠AOB=45°,半径OB=2,矩形PQRS的顶点P、S在半径OA上,Q在半径OB上,R在弧AB上,连接OR. 如图,∠C=90°,DE∥AB,EF⊥AB.找出图中所有相似三角形及位似三角形.
如图,∠C=90°,DE∥AB,EF⊥AB.找出图中所有相似三角形及位似三角形.