题目内容
6.为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题:
(1)求扇形统计图中m的值,并补全条形统计图;
(2)在被调查的学生中,随机抽一人,抽到选“体育特长类”或“艺术特长类”的学生的概率是多少?
(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理?
分析 (1)根据C类人数有15人,占总人数的25%可得出总人数,求出A类人数,进而可得出结论;
(2)直接根据概率公式可得出结论;
(3)求出“实践活动类”的总人数,进而可得出结论.
解答 解:(1)总人数=15÷25%=60(人).
A类人数=60-24-15-9=12(人).
∵12÷60=0.2=20%,
∴m=20.
条形统计图如图;
(2)抽到选“体育特长类”或“艺术特长类”的学生的概率=$\frac{24+9}{60}$=$\frac{11}{20}$;
(3)∵800×25%=200,200÷20=10,
∴开设10个“实验活动类”课程的班级数比较合理.
点评 本题考查的是条形统计图与扇形统计图,根据题意得出样本总数是解答此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
11.下列计算正确的是( )
| A. | (a2b)2=a2b2 | B. | a6÷a2=a3 | C. | (3xy2)2=6x2y4 | D. | (-m)7÷(-m)2=-m5 |
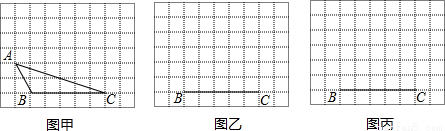
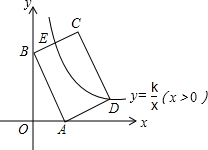 如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为(2,7).
如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为(2,7).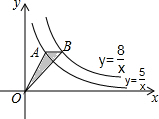 如图,点A在双曲线y=$\frac{5}{x}$上,点B在双曲线y=$\frac{8}{x}$上,且AB∥x轴,则△OAB的面积等于$\frac{3}{2}$.
如图,点A在双曲线y=$\frac{5}{x}$上,点B在双曲线y=$\frac{8}{x}$上,且AB∥x轴,则△OAB的面积等于$\frac{3}{2}$.