题目内容
15.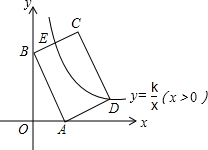 如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为(2,7).
如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为(2,7).
分析 首先过点D作DF⊥x轴于点F,易证得△AOB∽△DFA,然后由相似三角形的对应边成比例,求得点D的坐标,即可求得反比例函数的解析式,再利用平移的性质求得点C的坐标,继而求得直线BC的解析式,则可求得点E的坐标.
解答 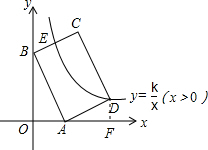 解:过点D作DF⊥x轴于点F,则∠AOB=∠DFA=90°,
解:过点D作DF⊥x轴于点F,则∠AOB=∠DFA=90°,
∴∠OAB+∠ABO=90°,
∵四边形ABCD是矩形,
∴∠BAD=90°,AD=BC,
∴∠OAB+∠DAF=90°,
∴∠ABO=∠DAF,
∴△AOB∽△DFA,
∴OA:DF=OB:AF=AB:AD,
∵AB:BC=3:2,点A(3,0),B(0,6),
∴AB:AD=3:2,OA=3,OB=6,
∴DF=2,AF=4,
∴OF=OA+AF=7,
∴点D的坐标为:(7,2),
∴反比例函数的解析式为:y=$\frac{14}{x}$①,点C的坐标为:(4,8),
设直线BC的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{b=6}\\{4k+b=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=6}\end{array}\right.$,
∴直线BC的解析式为:y=$\frac{1}{2}$x+6②,
联立①②得:$\left\{\begin{array}{l}{x=2}\\{y=7}\end{array}\right.$或$\left\{\begin{array}{l}{x=-14}\\{y=-1}\end{array}\right.$(舍去),
∴点E的坐标为:(2,7).
故答案为:(2,7).
点评 此题考查了反比例函数与一次函数的交点问题以及相似三角形的判定与性质.注意准确作出辅助线是解此题的关键.

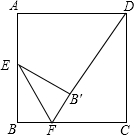 如图,正方形ABCD边长为2,E为AB边的中点,点F是BC边上一个动点,把△BEF沿EF向形内部折叠,点B的对应点为B′,当B′D的长最小时,BF长为( )
如图,正方形ABCD边长为2,E为AB边的中点,点F是BC边上一个动点,把△BEF沿EF向形内部折叠,点B的对应点为B′,当B′D的长最小时,BF长为( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$-1 | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{5}+1}{2}$ |
 如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的概率为( )
如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -3 | -2 | -3 | -6 | -11 | … |
| A. | 直线x=-3 | B. | 直线x=-2 | C. | 直线x=-1 | D. | 直线x=0 |

 已知:如图,四边形ABCD是平行四边形,延长BA至点E,使AE+CD=AD.连结CE,求证:CE平分∠BCD.
已知:如图,四边形ABCD是平行四边形,延长BA至点E,使AE+CD=AD.连结CE,求证:CE平分∠BCD.