题目内容
17.已知二元一次方程组$\left\{\begin{array}{l}{x-y=-5}\\{x+2y=-2}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-4}\\{y=1}\end{array}\right.$,则在同一平面直角坐标系中,直线l1:y=x+5与直线l2:y=-$\frac{1}{2}$x-1的交点坐标为(-4,1).分析 根据一次函数与二元一次方程组的关系进行解答即可.
解答 解:∵二元一次方程组$\left\{\begin{array}{l}{x-y=-5}\\{x+2y=-2}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-4}\\{y=1}\end{array}\right.$,
∴直线l1:y=x+5与直线l2:y=-$\frac{1}{2}$x-1的交点坐标为(-4,1),
故答案为:(-4,1).
点评 本题考查的是一次函数与二元一次方程组的关系,方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
10.已知函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是( )
| A. | 当a=1时,函数图象过点(-1,1) | |
| B. | 当a=-2时,函数图象与x轴没有交点 | |
| C. | 若a>0,则当x≥1时,y随x的增大而减小 | |
| D. | 若a<0,则当x≤1时,y随x的增大而增大 |
10. 如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的概率为( )
如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的概率为( )
 如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的概率为( )
如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
13.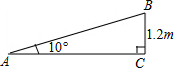 一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )
一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )
 一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )
一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )| A. | 斜坡AB的坡度是10° | B. | 斜坡AB的坡度是tan10° | ||
| C. | AC=1.2tan10°米 | D. | AB=$\frac{1.2}{cos10°}$米 |
9.在函数y=$\frac{\sqrt{x-3}}{x-4}$中,自变量x的取值范围是( )
| A. | x>3 | B. | x≥3 | C. | x>4 | D. | x≥3且x≠4 |
6.我国平均每平方千米的土地一年从太阳得到的能量,相当于燃烧130 000 000kg的煤所产生的能量.把130 000 000kg用科学记数法可表示为( )
| A. | 13×107kg | B. | 0.13×108kg | C. | 1.3×107kg | D. | 1.3×108kg |

 已知:如图,四边形ABCD是平行四边形,延长BA至点E,使AE+CD=AD.连结CE,求证:CE平分∠BCD.
已知:如图,四边形ABCD是平行四边形,延长BA至点E,使AE+CD=AD.连结CE,求证:CE平分∠BCD.