题目内容
4.化简$\frac{{a}^{2}+2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$-$\frac{b}{a-b}$的结果是$\frac{a}{a-b}$.分析 先将分母因式分解以确定最简公分母为(a+b)(a-b),再通分化为同分母分式,依据分式减法法则相减,最后将分式约分化成最简分式.
解答 解:原式=$\frac{{a}^{2}+2ab+{b}^{2}}{(a+b)(a-b)}$-$\frac{b(a+b)}{(a+b)(a-b)}$
=$\frac{{a}^{2}+2ab+{b}^{2}-ab-{b}^{2}}{(a+b)(a-b)}$
=$\frac{{a}^{2}+ab}{(a+b)(a-b)}$
=$\frac{a(a+b)}{(a+b)(a-b)}$
=$\frac{a}{a-b}$,
故答案为:$\frac{a}{a-b}$.
点评 本题主要考查分式的加减运算,异分母分式相加减,先通分,变为同分母分式,再利用同分母分式的加减法则计算,最后结果需是最简分式.

练习册系列答案
相关题目
14.在-(-3),(-2)2,0,-32,-|-3|中,负数的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
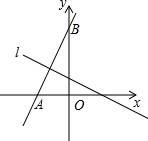 如图,己知直线y=2x+4与x轴,y轴分别交于A,B两点,则线段AB的中垂线l的函数表达式为y=$-\frac{1}{2}$x+$\frac{3}{2}$.
如图,己知直线y=2x+4与x轴,y轴分别交于A,B两点,则线段AB的中垂线l的函数表达式为y=$-\frac{1}{2}$x+$\frac{3}{2}$.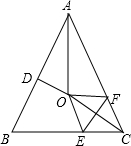 如图,在△ABC中,AB=AC,∠BAC=58°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠BEO的度数是64°.
如图,在△ABC中,AB=AC,∠BAC=58°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠BEO的度数是64°. 如图,AB=AC,∠BAC=90°,以AB为直径作⊙O,OC交⊙O于D,延长BD交AC于E,求$\frac{CE}{AE}$的值.
如图,AB=AC,∠BAC=90°,以AB为直径作⊙O,OC交⊙O于D,延长BD交AC于E,求$\frac{CE}{AE}$的值.