题目内容
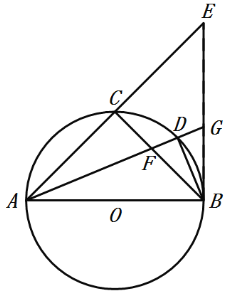
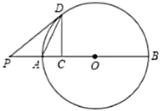
【题目】如图,点![]() 是
是![]() 直径
直径![]() 上一点,过
上一点,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,延长
,延长![]() 至点
至点![]() ,连接
,连接![]() ,使
,使![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析 (2)BC=12
【解析】
(1)求出∠ODA+∠PDA=∠ADC+∠DAO=90°,根据切线的判定得出即可;
(2)连接OD,求出∠PDC=∠DOC,解直角三角形求出![]() ,设DC=4x,OC=3x,求出3x+3=5x,求出x,即可得出答案.
,设DC=4x,OC=3x,求出3x+3=5x,求出x,即可得出答案.
(1)证明:连接OD,

∵OD=OA,
∴∠ODA=∠OAD,
∵CD⊥AB于点C,
∴∠OAD+∠ADC=90°,
∴∠ODA+∠ADC=90°,
∵∠PDA=∠ADC,
∴∠PDA+∠ODA=90°,
即∠PDO=90°,
∴PD⊥OD,
∵D在⊙O上,
∴PD是⊙O的切线;
(2) ∵∠PDO=90°,
∴∠PDC+∠CDO=90°,
∵CD⊥AB于点C,
∴∠DOC+∠CDO=90°,
∴∠PDC=∠DOC,
∵tan∠PDC=![]() ,
,
∴tan∠DOC=![]() =
=![]()
设DC=4x,CO=3x,则OD=5x,
∵AC=3,
∴OA=3x+3,
∴3x+3=5x,
∴x=![]()
∴OC=3x=![]()
OD=OB=5x=![]()
∴BC=12.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目