Question

5．“最美的女教师”张丽莉，为了抢救两名学生，以致双腿高位截肢，社会各界纷纷为她捐款．我市某中学八年级一班全体同学也积极参加了捐款活动，该班同学捐款情况的部分统计结果如图所示：

（1）求该班学生的总人数以及“捐款5元”所在扇形的圆心角的度数；
（2）请将条形统计图补充完整，并直接写出各捐款金额的众数；
（3）求该班平均每人捐款多少元？

Answer 1

分析 （1）由捐款15元的人数除以占的百分比，即可确定出该班学生的总人数；求出“捐款5元”的学生所占的百分比，再乘以360°即可得到“捐款5元”所在扇形的圆心角的度数；
（2）求出捐款10元、25元的人数，补全条形统计图，根据众数是一组数据中出现次数最多的数据求解即可；
（3）根据加权平均数的求解方法列式计算即可得解．

解答 解：（1）该班学生的总人数为：$\frac{14}{28%}$=50（名），
“捐款5元”所在扇形的圆心角的度数为：$\frac{10}{50}×360°=72°$；

（2）捐款10元的人数为：50×32%=16（人），
捐款25元的人数为：50-（10+16+14+6）=4（人），
画条形图，如图所示：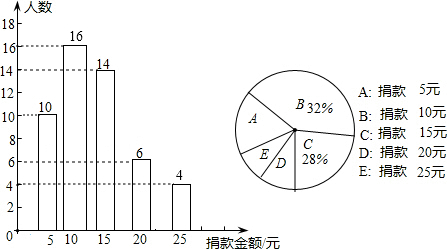

10元出现的次数最多，所以捐款金额的众数为：10元；

（3）该班平均每人捐款：$\frac{10×5+16×10+14×15+6×20+4×25}{50}=12.8$（元）．

点评 本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．