题目内容
类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做等邻边四边形.
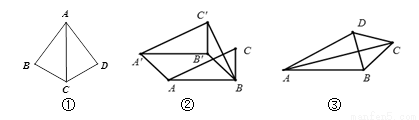
（1）如图①，四边形ABCD中，AC平分∠BAD，∠B=∠D. 求证：四边形ABCD为等邻边四边形.
（2）如图②，Rt△ABC中，∠ABC=90°，AB=2，BC=1，将△ABC沿∠ABC的平分线BB′的方向平移，得到△A′B′C′，连接AA′、BC′，若平移后的四边形ABC′A′是等邻边四边形，且满足BC′=AB，求平移的距离.
（3）如图③，在等邻边四边形ABCD中，AB=AD，∠BAD+∠BCD=90°，AC和BD为四边形对角线，△BCD为等边三角形，试探究AC和AB的数量关系.
练习册系列答案
名校通行证有效作业系列答案
相关题目
.
，求A的值.
，PD=10，则PE的长度为_____．
．
1．
已知△ABC和△ADE都是等腰直角三角形，∠ACB=∠ADE=90°，AC=2$\sqrt{2}$，AD=1，F是BE的中点．若将△ADE绕点A旋转一周，则线段AF长度的取值范围是（ ）
已知△ABC和△ADE都是等腰直角三角形，∠ACB=∠ADE=90°，AC=2$\sqrt{2}$，AD=1，F是BE的中点．若将△ADE绕点A旋转一周，则线段AF长度的取值范围是（ ）| A． | $\frac{4-\sqrt{2}}{2}$≤AF≤$\frac{4+\sqrt{2}}{2}$ | B． | 2≤AF≤3 | C． | $\frac{4-\sqrt{2}}{2}$≤AF≤3 | D． | $\frac{2-\sqrt{2}}{2}$≤AF≤$\frac{2+\sqrt{2}}{2}$ |