题目内容
1. 如图,矩形ABCD中,点E为对角线的交点,过点E的垂线交BC于点F,若AB=4,cos∠CEF=$\frac{4}{5}$,则△BEF的面积为5.
如图,矩形ABCD中,点E为对角线的交点,过点E的垂线交BC于点F,若AB=4,cos∠CEF=$\frac{4}{5}$,则△BEF的面积为5.
分析 如图连接DF,取DF的中点O,连接OE、OC.首先证明D、E、F、C四点共圆,推出∠FEC=∠FDC,可得cos∠FEC=cos∠FDC=$\frac{4}{5}$,推出$\frac{CD}{DF}$=$\frac{4}{5}$,推出DF=5,由BE=DE,FE⊥BD,推出BF=DF=5,可得S△BFD=$\frac{1}{2}$•BF•CD=10,由BE=DE,可得S△BFE=$\frac{1}{2}$S△BFD,即可解决问题.
解答 解:如图连接DF,取DF的中点O,连接OE、OC.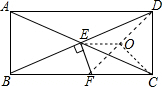
∵四边形ABCD是矩形,
∴∠BCD=90°,
∵OD=OF,∠DEF=90°,
∴OE=OD=OF=OC,
∴D、E、F、C四点共圆,
∴∠FEC=∠FDC,
∴cos∠FEC=cos∠FDC=$\frac{4}{5}$,
∴$\frac{CD}{DF}$=$\frac{4}{5}$,∵CD=4,
∴DF=5,
∵BE=DE,FE⊥BD,
∴BF=DF=5,
∴S△BFD=$\frac{1}{2}$•BF•CD=10,
∵BE=DE,
∴S△BFE=$\frac{1}{2}$S△BFD=5.
故答案为5.
点评 本题考查矩形的性质、锐角三角函数、四点共圆等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.

练习册系列答案
相关题目
13.若一个正多边形的每一个内角都等于120°,则它是( )
| A. | 正六边形 | B. | 正五边形 | C. | 正方形 | D. | 正八边形 |
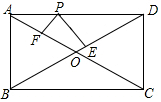 如图,矩形ABCD中,已知AD=4,AB=3,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,则PE+PF=( )
如图,矩形ABCD中,已知AD=4,AB=3,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,则PE+PF=( ) 在数轴上作出表示$\sqrt{20}$的点P(要求尺规作图,并保留痕迹).
在数轴上作出表示$\sqrt{20}$的点P(要求尺规作图,并保留痕迹). 如图,在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC绕点C逆时针旋转α(0°<α<90°),得到△MNC,连接BM,当BM⊥AC,则旋转角α的度数为60°.
如图,在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC绕点C逆时针旋转α(0°<α<90°),得到△MNC,连接BM,当BM⊥AC,则旋转角α的度数为60°. 如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,BD⊥OA,且OA•BD=$\frac{9}{2}$,则k的值为$\frac{3}{2}$.
如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,BD⊥OA,且OA•BD=$\frac{9}{2}$,则k的值为$\frac{3}{2}$.