题目内容
【题目】如图，在平面直角坐标系中，抛物线交
轴正半轴于点
（1，0）和点
，交
轴于点
．
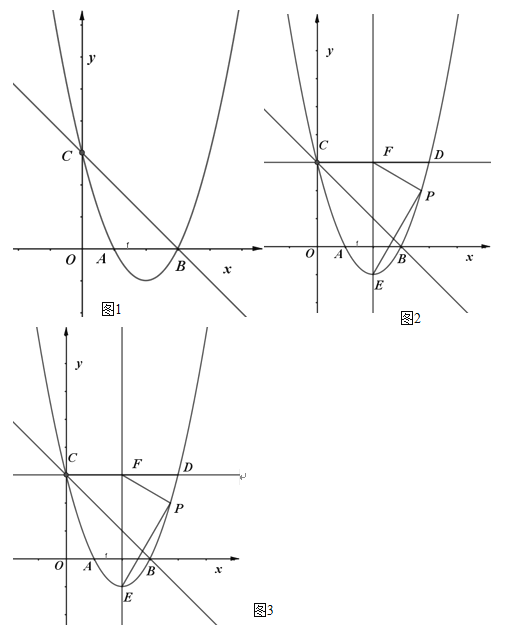
（1）如图1，直线
经过点、点，求抛物线的解析式；
（2）如图2，点
为该抛物线
的顶点，过点作轴的平行线交抛物线于另一点
，该抛物线对称轴右侧的抛物线上有一点
，当
时，求点的纵坐标．
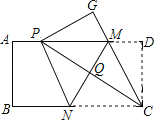
（3）如图3，在（1）（2）的结论下，抛物线对称轴右侧的抛物线上有一点
，作
轴于点
，延长
交
于
，当
时，求点的坐标．
【答案】（1）
；（2）点P的纵坐标为2；（3）
点的坐标为（
，11）．
【解析】
（1）由直线的解析式，先求出点B、C的坐标，结合点A的坐标，利用待定系数法即可得到答案；
（2）把点A代入，求出n的值，然后得到点C和点E的坐标，然后求出点F的坐标，设点P为（x，
），由
，即可求出点P的横坐标，即可求出点P的纵坐标；
（3）过点P作PI⊥GH于点I，先求出直线PE的解析式，得到PK=2PI，然后设点G为（m，
），表示出GK的长度，结合
，得到关于m的一元二次方程，解方程求出m的值，即可得到答案．
解：（1）∵
经过点
、点
，
∴令
，
，
令
，
，
∴点B为（3，0），点C为（0，3），
设抛物线的解析式为
，
把点A、B、C，三点代入解析式，得：
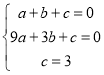，解得：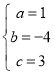
，
∴；
（2）∵点A（1，0）在抛物线
图像上，则
，
∴
，
∴
，
∴顶点E为（2，
），
令x=0，则，
∴点C为（0，3），
∵EF垂直平分CD，
∴点D的坐标为（4，3），点F的坐标为（2，3），
∵点P在抛物线上，则设点P为（x，
），
又∵E为（2，），F为（2，3），
∴
，
，
∵，
∴
，
∴
，
解得：
，
∵点P在对称轴右侧，则
，
∴点P的横坐标为
，
∴点P的纵坐标为：
；
（3）如图：过点P作PI⊥GH于点I，
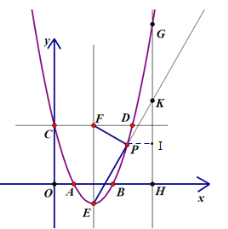
∵点E（2，），点P为（
，2），
∴可求出直线PE的解析式为：
，
∴∠KPI=60°，
∵PI⊥GH，
∴∠KIP=90°，∠PKI=30°，
∴PK=2PI，
∵点G在抛物线图像上，
则设点G为（m，），
∴点K的坐标为（m，
）
∴GK=
；
∵第P的坐标为（，2），
∴点I的坐标为（m，），
∴PI=
，
∴PK=
，
∵，
∴
，
解得：
，
，
当
时，点G与点P、点K重合，
∴
；不符合题意，舍去；
∴点G的横坐标为；
∴点G的纵坐标为：
，
∴点G的坐标为（，11）．
