��Ŀ����
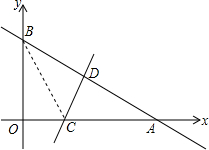 ��ͼ��һ�κ���y=-
��ͼ��һ�κ���y=-| 3 |
| 4 |
��1����A������Ϊ
��2����OC�ij��ȣ�
��3��������P��Q�ֱ�ӵ�O��Aͬʱ��ʼ�˶�����P��ÿ��1����λ���ٶ���O��A�˶�����Q��ÿ��2����λ���ٶ���A��B�˶����κ�һ�㵽���յ��˶���ֹͣ�������˶�ʱ��Ϊt��ʱ����APQΪ���������Σ���д��t�����п���ֵ��
���㣺һ�κ����ۺ���
ר�⣺
��������1����y=0���x��ֵ������x=0���y��ֵ�������A��B��������ꣻ
��2��OC=x�����ݷ��۱任��������x��ʾ��BC�ij����ٸ��ݹ��ɶ�����⼴�ɣ�
��3������x���ϵ�������ص����P������꣬�ٸ��������ľ��빫ʽ��ɣ�
��2��OC=x�����ݷ��۱任��������x��ʾ��BC�ij����ٸ��ݹ��ɶ�����⼴�ɣ�
��3������x���ϵ�������ص����P������꣬�ٸ��������ľ��빫ʽ��ɣ�
����⣺��1����y=0����x=4����x=0����y=4��
�ʵ�A������Ϊ��4��0������B������Ϊ��0��3����
�ʴ��ǣ�4��0������0��3����
��2����OC=x����AC=CB=4-x��
�ߡ�BOA=90�㣬
��OB2+OC2=CB2��
32+x2=��4-x��2��
��ã�x=
��
��OC=
��
��3����P��������x��0����
��PA=PQʱ����x-4��2=x2+9�����x=
��
��PA=AQʱ����x-4��2=42+32�����x=9��x=-1����ȥ����
��PQ=AQʱ��x2+32=42+32�����x=-4����ȥ����
��P�������ǣ�
��0����9��0����
��t=
��t=9��
�ʵ�A������Ϊ��4��0������B������Ϊ��0��3����
�ʴ��ǣ�4��0������0��3����
��2����OC=x����AC=CB=4-x��
�ߡ�BOA=90�㣬
��OB2+OC2=CB2��
32+x2=��4-x��2��
��ã�x=
| 7 |
| 8 |
��OC=
| 7 |
| 8 |
��3����P��������x��0����
��PA=PQʱ����x-4��2=x2+9�����x=
| 7 |
| 8 |
��PA=AQʱ����x-4��2=42+32�����x=9��x=-1����ȥ����
��PQ=AQʱ��x2+32=42+32�����x=-4����ȥ����
��P�������ǣ�
| 7 |
| 8 |
��t=
| 7 |
| 8 |
������������һ�κ����빴�ɶ������������ϵĵ���ص㣬�Լ�����֮��ľ��빫ʽ���ۺ�Ӧ�ã��ڽ���ʱע��������ۣ�����©�⣮

��ϰ��ϵ�д�
�����Ŀ
���㣨-2��-4����ֱ���ǣ�������
| A��y=x-2 |
| B��y=x+2 |
| C��y=2x+1 |
| D��y=-2x+1 |
 ��7����ͬ���ⳤΪ2��С�������ɵļ�������ͼ��ʾ��
��7����ͬ���ⳤΪ2��С�������ɵļ�������ͼ��ʾ�� ��ͼ�������˶�Ավ�ڵ�O����ϰ������ӵ�O���Ϸ�2�ĵ�A���������ɵ㣬�����еĸ߶�y���ף������е�ˮƽ����x���ף������ϵʽy=a��x-6��2+h����֪�������O��ˮƽ����Ϊ9�ף��߶�Ϊ2.43�ף��ı߽���O��ˮƽ����Ϊ18�ף�
��ͼ�������˶�Ավ�ڵ�O����ϰ������ӵ�O���Ϸ�2�ĵ�A���������ɵ㣬�����еĸ߶�y���ף������е�ˮƽ����x���ף������ϵʽy=a��x-6��2+h����֪�������O��ˮƽ����Ϊ9�ף��߶�Ϊ2.43�ף��ı߽���O��ˮƽ����Ϊ18�ף�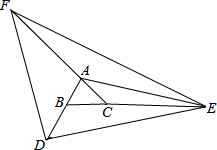 ��ͼ���ӳ��ȱߡ�ABC�ı�AB��D��ʹBD=3���ӳ�BC��E��ʹCE=4���ӳ�CA��F��ʹAF=5������DEF�����Ϊ
��ͼ���ӳ��ȱߡ�ABC�ı�AB��D��ʹBD=3���ӳ�BC��E��ʹCE=4���ӳ�CA��F��ʹAF=5������DEF�����Ϊ