题目内容
20. 如图,直线AB、CD相交于O,OE⊥OF,OC平分∠AOE,且∠BOF=2∠BOE,则∠BOD=75°.
如图,直线AB、CD相交于O,OE⊥OF,OC平分∠AOE,且∠BOF=2∠BOE,则∠BOD=75°.
分析 首先根据OE⊥OF,∠BOF=2∠BOE,求出∠BOE=30°;然后求出∠AOE=150°,再根据OC平分∠AOE,求出∠AOC的度数;最后根据∠BOD和∠AOC互为对顶角,求出∠BOD的度数是多少即可.
解答 解:∵OE⊥OF,
∴∠EOF=90°,
∵∠BOF=2∠BOE,
∴3∠BOE=90°,
∴∠BOE=90°÷3=30°,
∴∠AOE=180°-∠BOE=180°-30°=150°,
又∵OC平分∠AOE,
∴∠AOC=$\frac{1}{2}$∠AOE=$\frac{1}{2}×150°$=75°,
∵∠BOD和∠AOC互为对顶角,
∴∠BOD=∠AOC=75°.
故答案为:75°.
点评 (1)此题主要考查了垂线的性质和应用,要熟练掌握,解答此题的关键是要明确垂线的性质:在平面内,过一点有且只有一条直线与已知直线垂直.
(2)此题还考查了对顶角和邻补角的特征和应用,要熟练掌握,解答此题的关键是要明确:①有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.②补角互补,即和为180°.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
15.实数9的算术平方根是( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 81 |
13.计算$\frac{1}{x-1}$+$\frac{x}{1-x}$的结果是( )
| A. | x-1 | B. | 1-x | C. | 1 | D. | -1 |
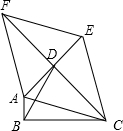 定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径,即损矩形外接圆的直径.如图,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,点D是菱形ACEF对角线的交点,连接BD.若∠DBC=60°,∠ACB=15°,BD=2$\sqrt{3}$,则菱形ACEF的面积为12$\sqrt{3}$.
定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径,即损矩形外接圆的直径.如图,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,点D是菱形ACEF对角线的交点,连接BD.若∠DBC=60°,∠ACB=15°,BD=2$\sqrt{3}$,则菱形ACEF的面积为12$\sqrt{3}$. 小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问:从小华家到学校的平路和下坡路各有多远?
小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问:从小华家到学校的平路和下坡路各有多远?