题目内容
16.如图,在菱形ABCD中,AC=8cm,BD=6cm,第一次平移将菱形ABCD沿射线AC方向向右平移6cm得菱形A1B1C1D1,第二次平移将菱形A1B1C1D1沿射线AC方向向右平移6cm得菱形A2B2C2D2,…第n次平移将菱形An-1Bn-1Cn-1Dn-1沿射线AC方向向右平移6cm得菱形AnBnCnDn,(n>2)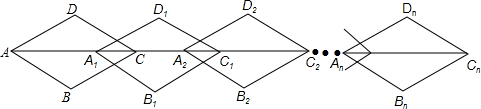
(1)填空:AC1=14,AC2=20,ACn=6n+8;
(2)若ACn的长为68cm,求n.
分析 (1)根据平移的性质得出AA1=6cm,A1A2=6cm,A2C1=A1C1-A1A2=8-6=2,进而求出AC1和AC2的长,再得到一般性规律即可求出ACn的长;
(2)根据(1)中所求得出数字变化规律,进而得出ACn=(n+1)×6+2=68,求出n即可.
解答 解:(1)∵AC=8cm,BD=6cm,第一次平移将菱形ABCD沿射线AC方向向右平移6cm得菱形A1B1C1D1,第二次平移将菱形A1B1C1D1沿射线AC方向向右平移6cm得菱形A2B2C2D2,
∴AA1=6cm,A1A2=6cm,A2C1=A1C1-A1A2=8-6=2,
∴AC1=AA1+A1A2+A2C1=6+6+2=14,
∴AB2的长为:6+6+6+2=20,
∴ACn=(n+1)×6+2=6n+8,
故答案为:14,20,6n+8;
(2)∵ACn=(n+1)×6+2,
∴(n+1)×6+2=68,
解得:n=10.
点评 此题综合考查了平移的性质、菱形的性质和相似多边形的性质,根据平移的性质得到ACn=(n+1)×6+2这一规律是解题关键.

练习册系列答案
相关题目
5.若a<1,则(a-1)x+1>0的解集为( )
| A. | x>$\frac{1}{a-1}$ | B. | x<$\frac{1}{a-1}$ | C. | x>-$\frac{1}{1-a}$ | D. | x<$\frac{1}{1-a}$ |
8.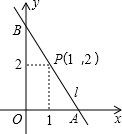 如图,直线l经过点P(1,2)与坐标轴交于A(a,0),B(0,b)两点(其中a<b),如果a+b=6,那么tan∠ABO的值为( )
如图,直线l经过点P(1,2)与坐标轴交于A(a,0),B(0,b)两点(其中a<b),如果a+b=6,那么tan∠ABO的值为( )
 如图,直线l经过点P(1,2)与坐标轴交于A(a,0),B(0,b)两点(其中a<b),如果a+b=6,那么tan∠ABO的值为( )
如图,直线l经过点P(1,2)与坐标轴交于A(a,0),B(0,b)两点(其中a<b),如果a+b=6,那么tan∠ABO的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
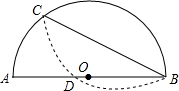 如图,BC为半圆中一条非直径的弦,现将$\widehat{BC}$沿弦BC对对折后交直径AB于点D,若AB=10,CB=4$\sqrt{5}$,则$\frac{AD}{DB}$的值为$\frac{2}{3}$.
如图,BC为半圆中一条非直径的弦,现将$\widehat{BC}$沿弦BC对对折后交直径AB于点D,若AB=10,CB=4$\sqrt{5}$,则$\frac{AD}{DB}$的值为$\frac{2}{3}$.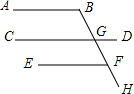 如图,CD与BH相交于点G,∠B=∠BGD,∠DGF=∠BFE,求证:∠B=∠EFH(请先完成下面的填空,再继续完成此题的证明)
如图,CD与BH相交于点G,∠B=∠BGD,∠DGF=∠BFE,求证:∠B=∠EFH(请先完成下面的填空,再继续完成此题的证明)