Question

8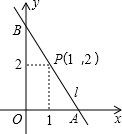．如图，直线l经过点P（1，2）与坐标轴交于A（a，0），B（0，b）两点（其中a＜b），如果a+b=6，那么tan∠ABO的值为（　　）

• A． $\frac{1}{2}$
• B． 1
• C． $\frac{3}{2}$
• D． 2

Answer 1

分析 根据题意得出b=2-k，a=4+k，进而代入函数关系式求出k的值进而求出a，b的值即可得出答案．

解答 解：设直线AB的解析式为：y=kx+b，则将（1，2）点代入得：
k+b=2，
∴b=2-k，
∵a+b=6，k+b=2，
∴a=4+k，
∵直线l经过点P（1，2），与坐标轴交于A（a，0），
∴ak+b=0，
∴（4+k）k+2-k=0，
解得：k₁=-1，k₂=-2，
当k=-1，则a=3，b=3，不合题意舍去；
∴k=-2，则a=2，b=4，
∴tan∠ABO的值为：$\frac{2}{4}=\frac{1}{2}$．
故选：A．

点评 此题主要考查了一函数图象上点的坐标性质以及锐角三角函数关系等知识，得出关于k的一元二次方程是解题关键．