Question

6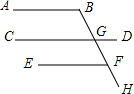．如图，CD与BH相交于点G，∠B=∠BGD，∠DGF=∠BFE，求证：∠B=∠EFH（请先完成下面的填空，再继续完成此题的证明）
证明：∵∠B=∠BGD（已知）
∴AB∥CD（内错角相等，两直线平行）

Answer 1

分析 根据平行线的判定可先证明AB∥CD，CD∥EF，再根据平行线的传递性可证明AB∥EF，可证明∠B=∠EFH．

解答 证明：
∵∠B=∠BGD（已知）
∴AB∥CD（ 内错角相等，两直线平行），
∵∠DGF=∠BFE，
∴CD∥EF，
∴AB∥EF，
∴∠B=∠EFH．
故答案为：内错角相等，两直线平行．

点评 本题主要考查平行线的判定和性质，掌握平行线的判定和性质是解题的关键，即①同位角相等?两直线平行，②内错角相等?两直线平行，③同旁内角互补?两直线平行，④a∥b，b∥c⇒a∥c．