题目内容
某玩具厂计划生产一
种玩具熊猫，每日最高产量为40只，且每日产出的产品全部售出，已知
生产x只熊猫的成本为R元，售价为每只P元，且R，P与x之间的函数关系式分别为R＝500＋30x，P＝170－2x.
(1)当日产量为多少只时，每日获得的利润为1750元?
(2)当日产量为多少只时，每日可获得最大利润?最大利润是多少元?
解：设每日利润是y元，则y＝Px－R=x(170－2x)－(500＋30x)=－2x2＋140x－500=－2(x－35)2＋1950(其中0＜x≤40，且x为整数)．(1)当y=1750时，－2x2＋140x－500＝1750，解得x1＝25，x2=45(舍去)，∴当日产量为25只时，每日获得的利润为1750元． (2)∵y＝－2(x－35)2＋1950，∴当日产量为35只时，每日可获得最大利润，为1950元．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
图2-3中的三角形是有规律地从里到外逐层排列的．设y为第n层(n为正整数)三角形的个数，则下列函数关系式正确的是 ( )
n＋
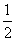x2－x＋
.
．
09所示的抛物线的解析式是 ( )
中点到AB的距离CD的长，就能求出这个圆形工件的半径.你认为他的做法合理吗？如不合理，说明理由；如合理，请你给出具体的数值，求出半径。