题目内容
6．已知二次函数y=-8（x+m）2+n的图象的顶点坐标是（-5，-4），那么一次函数y=mx+n的图象经过第一、三、四象限．分析 由二次函数y=-8（x+m）2+n的图象的顶点坐标是（-5，-4），得出m=5，n=-4，进一步利用一次函数的性质得出答案即可．
解答 解：∵y=-8（x+m）2+n的图象的顶点坐标是（-5，-4），
∴m=5，n=-4，
∴一次函数y=5x-4，
∴图象经过一、三、四象限．
故答案为：一、三、四．
点评 此题考查二次函数的图象与性质、一次函数的图象与性质，关键是根据抛物线的顶点坐标求得m、n的数值．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
17．将2x2-x-2分解因式为（ ）
| A． | $（{x-\frac{1}{4}+\frac{{\sqrt{17}}}{4}}）（{x-\frac{1}{4}-\frac{{\sqrt{17}}}{4}}）$ | B． | $2（{x+\frac{1}{4}-\frac{{\sqrt{17}}}{4}}）（{x-\frac{1}{4}-\frac{{\sqrt{17}}}{4}}）$ | ||
| C． | $2（{x-\frac{1}{4}+\frac{{\sqrt{17}}}{4}}）（{x+\frac{1}{4}-\frac{{\sqrt{17}}}{4}}）$ | D． | $2（{x-\frac{1}{4}+\frac{{\sqrt{17}}}{4}}）（{x-\frac{1}{4}-\frac{{\sqrt{17}}}{4}}）$ |
如图所示，?ABCD中，∠ADC和∠BCD的平分线交于点M，且分别交AB于E、F．
1．已知抛物线y=-2x2+12x-13，则下列关于此抛物线说法正确的是（ ）
| A． | 开口向下，对称轴为直线x=-3 | B． | 顶点坐标为（-3，5） | ||
| C． | 最小值为5 | D． | 当x＞3时，y随x的增大而减小 |
已知在纸面上有一数轴（如图），折叠纸面．
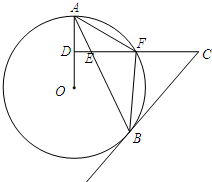如图，AB是⊙O的弦，D为半径OA的中点，过D作CD⊥OA交弦AB于点E，交⊙O于点F，且CE=CB．