题目内容
 已知△ABC和△DEF都是边长为10cm的等边三角形,且BCDE在同一直线上,连接AD、CF.若BD=3cm,△ABC沿着BE的方向以每秒1cm的速度运动,设△ABC运动时间为t.
已知△ABC和△DEF都是边长为10cm的等边三角形,且BCDE在同一直线上,连接AD、CF.若BD=3cm,△ABC沿着BE的方向以每秒1cm的速度运动,设△ABC运动时间为t.(1)当t为何值时,四边形ADFC是菱形.
(2)当t为何值时,平行四边形ADFC是矩形,并求其面积.
(3)当t为何值时,平行四边形ADFC的面积是100
| 3 |
考点:菱形的判定,等边三角形的性质,平行四边形的性质,矩形的判定
专题:
分析:(1)根据已知条件可知AC∥DF,即可得出四边形ADFC是平行四边形,根据△ABC沿着BE的方向以每秒1cm的速度运动,所以当t=
=3秒时,B与D重合,这时四边形为菱形,
(2)若平行四边形ADFC是矩形,则∠ADF=90°,E与B重合,得出t=13秒,可求出此时矩形的面积;
(3)分B、D重合前,B、D重合时,B、D重合后三种情况讨论求解.
| 3 |
| 1 |
(2)若平行四边形ADFC是矩形,则∠ADF=90°,E与B重合,得出t=13秒,可求出此时矩形的面积;
(3)分B、D重合前,B、D重合时,B、D重合后三种情况讨论求解.
解答: 解:(1)当t=3秒时,?ADFC是菱形.理由如下:
解:(1)当t=3秒时,?ADFC是菱形.理由如下:
∵△ABC和△DEF是两个边长为10cm的等边三角形.
∴AC=DF,∠ACD=∠FDE=60°
∴AC∥DF
∴四边形ADFC是平行四边形
当t=3秒时,?ADFC是菱形.
此时B与D重合,∴AD=DF,
∴?ADFC是菱形;
(2)当t=13秒时,?ADFC是矩形.理由如下:
此时B与E重合,
∴AF=CD,
∴?ADFC是矩形,
∴∠CFD=90°,CF=
∴S矩形ADFC=10×10
=100
cm2;
(3)①B、D重合前,(7-t)×5
÷2×2=100
,解得t=-13(不合题意所求);
②B、D重合时,t=3,10×5
÷2×2=100
(不合题意所求);
③B、D重合后,(t+7)×5
÷2×2=100
,解得t=13.
综上所述,当t为13秒时,平行四边形ADFC的面积是100
cm2.
 解:(1)当t=3秒时,?ADFC是菱形.理由如下:
解:(1)当t=3秒时,?ADFC是菱形.理由如下:∵△ABC和△DEF是两个边长为10cm的等边三角形.
∴AC=DF,∠ACD=∠FDE=60°
∴AC∥DF
∴四边形ADFC是平行四边形
当t=3秒时,?ADFC是菱形.
此时B与D重合,∴AD=DF,
∴?ADFC是菱形;
(2)当t=13秒时,?ADFC是矩形.理由如下:
此时B与E重合,
∴AF=CD,
∴?ADFC是矩形,
∴∠CFD=90°,CF=
| CD2-DF2 |
∴S矩形ADFC=10×10
| 3 |
| 3 |
(3)①B、D重合前,(7-t)×5
| 3 |
| 3 |
②B、D重合时,t=3,10×5
| 3 |
| 3 |
③B、D重合后,(t+7)×5
| 3 |
| 3 |
综上所述,当t为13秒时,平行四边形ADFC的面积是100
| 3 |
点评:本题考查了矩形的性质及其应用,考查了菱形的判定,以及菱形与矩形的区别论证及其计算.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
某排球队12名队员的年龄如表:
该队队员年龄的众数与中位数分别是( )
| 年龄/岁 | 19 | 20 | 21 | 22 | 23 |
| 人数/人 | 1 | 4 | 3 | 2 | 2 |
| A、19岁,20岁 |
| B、20岁,20岁 |
| C、20岁,21岁 |
| D、21岁,22岁 |
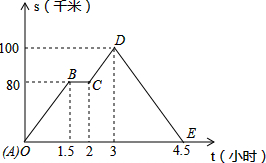 如图:图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,回答:
如图:图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,回答: 已知A、B在数轴上分别表示a、b
已知A、B在数轴上分别表示a、b 已知:如图,∠B=∠C,AD平分∠BAC,DE⊥AB,DF⊥AC,求证:BE=CF.
已知:如图,∠B=∠C,AD平分∠BAC,DE⊥AB,DF⊥AC,求证:BE=CF.