题目内容
 已知:如图,∠B=∠C,AD平分∠BAC,DE⊥AB,DF⊥AC,求证:BE=CF.
已知:如图,∠B=∠C,AD平分∠BAC,DE⊥AB,DF⊥AC,求证:BE=CF.考点:角平分线的性质,全等三角形的判定与性质
专题:证明题
分析:根据角平分线上的点到角的两边距离相等可得DE=DF,再利用“角角边”证明△BDE和△CDF全等,根据全等三角形对应边相等证明即可.
解答:证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(AAS),
∴BE=CF.
∴DE=DF,∠BED=∠CFD=90°,
在△BDE和△CDF中,
|
∴△BDE≌△CDF(AAS),
∴BE=CF.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,证明边相等,利用边所在的三角形全等证明是常用的方法,要熟练掌握并灵活运用.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
化简分式
的结果是( )
| a2-ab |
| b2-a2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知△ABC和△DEF都是边长为10cm的等边三角形,且BCDE在同一直线上,连接AD、CF.若BD=3cm,△ABC沿着BE的方向以每秒1cm的速度运动,设△ABC运动时间为t.
已知△ABC和△DEF都是边长为10cm的等边三角形,且BCDE在同一直线上,连接AD、CF.若BD=3cm,△ABC沿着BE的方向以每秒1cm的速度运动,设△ABC运动时间为t.
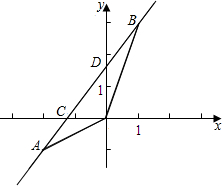 如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D. 如图,已知:△ABC中,∠C=90°,D、E是AB边上的两点,且AD=AC,BE=BC.求∠DCE的度数.
如图,已知:△ABC中,∠C=90°,D、E是AB边上的两点,且AD=AC,BE=BC.求∠DCE的度数.