题目内容
15.已知二次函数y=ax2+bx+c的图象与x轴交于点(-1,0),(x1,0),且1<x1<2,与y轴的正半轴的交点在(0,1)的下方.下列结论:①a-b+c=0,②0<b<-a,③a+c>0,④a-b+1>0,其中正确结论的个数是4个.分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 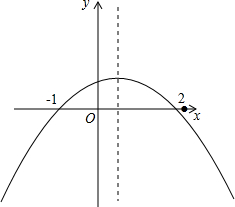 解:如图,
解:如图,
①当x=-1时,y=0,即a-b+c=0,故①正确;
②∵抛物线开口方向向下,
∴a<0,
又0<-$\frac{b}{2a}$<$\frac{2-1}{2}$,
∴0<b<-a,故②正确;
③∵二次函数y=ax2+bx+c(a>0)的图象与x轴交于点(-1,0),
∴a-b+c=0,
即a+c=b,
∵b>0,
∴a+c>0,故③正确;
④∵该抛物线与y轴的正半轴的交点在(0,1)的下方,
∴c<1,
∴0=a-b+c<a-b+1,即a-b+1>0,故④正确.
综上所述,正确的结论有:4个.
故答案是:4.
点评 主要考查图象与二次函数系数之间的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
相关题目
3.据有关部门统计,目前地球上水的总储量约为1.36×1018m3,其中可供人类使用的淡水只占0.3%左右,根据以上信息可以计算出地球上可供人类使用的淡水的总量,将计算结果用科学记数法表示为( )
| A. | 4.08×1014 | B. | 4.08×1015 | C. | 4.08×1016 | D. | 4.08×1017 |
20.今年国庆假期,客流最高峰出现在10月1日,铁路当天发送游客1330万人次,比去年同日最高峰增长13.4%,将1330万用科学记数法表示为( )
| A. | 0.133×104万 | B. | 1.33×103万 | C. | 1.33×104万 | D. | 13.3×102万 |
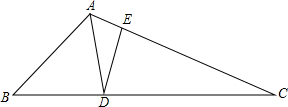 如图,已知△ABC,AD平分∠BAC,DE垂直AC,垂足为E,∠ADB=2∠B=4∠C,AE=$\frac{3}{4}$,CD=$\frac{7}{2}$,则线段AB=$\frac{55}{26}$.
如图,已知△ABC,AD平分∠BAC,DE垂直AC,垂足为E,∠ADB=2∠B=4∠C,AE=$\frac{3}{4}$,CD=$\frac{7}{2}$,则线段AB=$\frac{55}{26}$.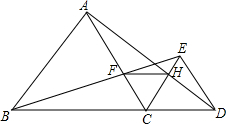 如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,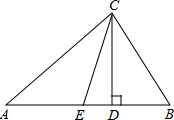 如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.
如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.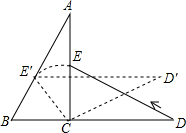 两块大小一样斜边为4且含有30°角的三角板如图5水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB上时,△CDE旋转了30°.
两块大小一样斜边为4且含有30°角的三角板如图5水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB上时,△CDE旋转了30°.