题目内容
2.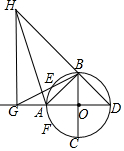 设AD、BC是圆O的互相垂直的直径,E和F分别在劣弧$\widehat{AB}$,$\widehat{CA}$上,若$\widehat{AE}$和$\widehat{AF}$相等,直线DA和直线BE的交点为G,直线FA和直线DB的交点为H,求证:∠HGA是直角.
设AD、BC是圆O的互相垂直的直径,E和F分别在劣弧$\widehat{AB}$,$\widehat{CA}$上,若$\widehat{AE}$和$\widehat{AF}$相等,直线DA和直线BE的交点为G,直线FA和直线DB的交点为H,求证:∠HGA是直角.
分析 连接AC、AE、CF、DE,由AD、BC是圆O的互相垂直的直径,得出AB=AC,AB⊥DE,∠CAD=∠BAD=∠BED=45°,$\widehat{AE}=\widehat{AF}$,$\widehat{AB}=\widehat{AC}$,得出$\widehat{BE}=\widehat{CF}$,由圆周角定理得出∠BAE=∠CAF=∠BDE,由角的关系得出∠HAG=∠HBG,证出H、G、A、B四点共圆,即可得出结论.
解答 证明:连接AC、AE、CF、DE,如图所示: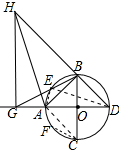
∵AD、BC是圆O的互相垂直的直径,
∴AB=AC,AB⊥DE,∠CAD=∠BAD=∠BED=45°,
∵$\widehat{AE}=\widehat{AF}$,$\widehat{AB}=\widehat{AC}$,$\widehat{BE}=\widehat{CF}$,
∴∠BAE=∠CAF=∠BDE,
∵∠HAG=∠DAF=∠CAD+∠CAF=45°+∠CAF,∠HBG=∠BED+∠BDE=45°+∠BDE,
∴∠HAG=∠HBG,
∴H、G、A、B四点共圆,
∴∠HGA=∠HBA=90°.
点评 本题考查了圆周角定理、四点共圆等知识;熟练掌握圆周角定理,证明四点共圆是解决问题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
17.下列说法中正确的个数有( )
①三点确定一个圆;
②平分弦的直径垂直于弦;
③三角形的外心到三角形三边的距离相等;
④等弧所对的圆周角相等;
⑤以3、4、5为边的三角形,其内切圆的半径是1.
①三点确定一个圆;
②平分弦的直径垂直于弦;
③三角形的外心到三角形三边的距离相等;
④等弧所对的圆周角相等;
⑤以3、4、5为边的三角形,其内切圆的半径是1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.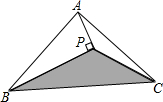 如图,△PBC的面积为10cm2,AP垂直∠B的平分线BP于P,则△ABC的面积为( )
如图,△PBC的面积为10cm2,AP垂直∠B的平分线BP于P,则△ABC的面积为( )
 如图,△PBC的面积为10cm2,AP垂直∠B的平分线BP于P,则△ABC的面积为( )
如图,△PBC的面积为10cm2,AP垂直∠B的平分线BP于P,则△ABC的面积为( )| A. | 10cm2 | B. | 12cm2 | C. | 16cm2 | D. | 20cm2 |
 已知四边形ABCD,四边形DEFG都是正方形,H是BF中点,I是AG中点,求证:AG=2HI.
已知四边形ABCD,四边形DEFG都是正方形,H是BF中点,I是AG中点,求证:AG=2HI.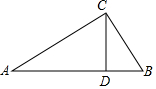 如图,在 Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求:
如图,在 Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求: 我们已经知道:
我们已经知道: